题目内容
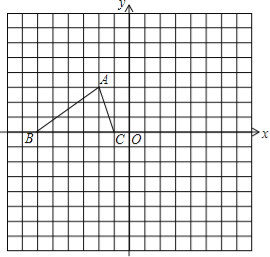
【题目】如图,在直角坐标系中,点![]() 在直线
在直线![]() 上,点
上,点![]() 、
、![]() 的坐标分别是(-1,0),(1,2),点
的坐标分别是(-1,0),(1,2),点![]() 的横坐标为2,过点
的横坐标为2,过点![]() 作
作![]() 轴于
轴于![]() ,过点
,过点![]() 作
作![]() 轴于
轴于![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)若![]() ,
, ![]() ,求
,求![]() (用
(用![]() ,
, ![]() 表示);
表示);
(2)已知直线![]() 上的点的横坐标
上的点的横坐标![]() 与纵坐标
与纵坐标![]() 都是二元一次方程
都是二元一次方程![]() 的解(同学们可以用点
的解(同学们可以用点![]() 、
、![]() 的坐标进行检验),直线
的坐标进行检验),直线![]() 上的点的横坐标
上的点的横坐标![]() 与纵坐标
与纵坐标![]() 都是二元一次方程
都是二元一次方程![]() 的解,求点
的解,求点![]() 、
、![]() 的坐标;
的坐标;
(3)解方程组![]() ,比较该方程组的解与两条直线的交点
,比较该方程组的解与两条直线的交点![]() 的坐标,你得出什么结论?
的坐标,你得出什么结论?

【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标为(2,3);点
的坐标为(2,3);点![]() 的坐标是(0,4); (3)直线
的坐标是(0,4); (3)直线![]() 与直线
与直线![]() 的交点坐标就是方程组
的交点坐标就是方程组![]() 的解.
的解.
【解析】(1)∵![]() 轴,
轴, ![]() 轴,
轴,
∴![]() ∥
∥![]() , 1分
, 1分
∴![]() ,
, ![]() ,
,
∴![]() ; 3分
; 3分
(2)∵点![]() 的横坐标为2,把
的横坐标为2,把![]() 代入方程
代入方程![]() ,
,
解得![]() ,∴点
,∴点![]() 的坐标为(2,3); 4分
的坐标为(2,3); 4分
∵点![]() 在
在![]() 轴上,∴点
轴上,∴点![]() 的横坐标为0, 5分
的横坐标为0, 5分
把![]() 代入
代入![]() ,解得
,解得![]() ,∴点
,∴点![]() 的坐标是(0,4); 6分
的坐标是(0,4); 6分
(3)方程组![]() 的解是
的解是![]() , 7分
, 7分
∵点![]() 的坐标是(1,2),
的坐标是(1,2),
∴直线![]() 与直线
与直线![]() 的交点坐标就是方程组
的交点坐标就是方程组![]() 的解.
的解.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
【题目】某跳远队准备从甲、乙、丙、丁4名运动员中选取成绩好且稳定的一名选手参赛,经测试,他们的成绩如下表,综合分析应选
成绩 | 甲 | 乙 | 丙 | 丁 |
平均分(单位:米) | 6.0 | 6.1 | 5.5 | 4.6 |
方差 | 0.8 | 0.2 | 0.3 | 0.1 |
A. 甲B. 乙C. 丙D. 丁