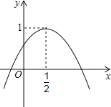题目内容
【题目】在平面直角坐标系![]() 中(如图),已知抛物线
中(如图),已知抛物线![]() 经过
经过![]() ,
,![]() ,顶点为
,顶点为![]() .
.
![]() 求该抛物线的表达方式及点
求该抛物线的表达方式及点![]() 的坐标;
的坐标;
![]() 将
将![]() 中求得的抛物线沿
中求得的抛物线沿![]() 轴向上平移
轴向上平移![]() 个单位,所得新抛物线与
个单位,所得新抛物线与![]() 轴的交点记为点
轴的交点记为点![]() .当
.当![]() 时等腰三角形时,求点
时等腰三角形时,求点![]() 的坐标;
的坐标;
![]() 若点
若点![]() 在
在![]() 中求得的抛物线的对称轴上,联结
中求得的抛物线的对称轴上,联结![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针转
逆时针转![]() 得到线段
得到线段![]() ,若点
,若点![]() 恰好落在
恰好落在![]() 中求得的抛物线上,求点
中求得的抛物线上,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;顶点
;顶点![]() 坐标为
坐标为![]() ;(2)
;(2)![]() 坐标为
坐标为![]() ;(3)
;(3)![]() 的坐标为
的坐标为![]() ,
,![]() .
.
【解析】
(1)将A与B坐标代入抛物线解析式中求出a与c的值,即可确定出抛物线解析式,配方后即可求出顶点C的坐标;
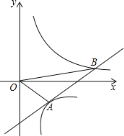
(2)由平移规律即C的坐标表示出D的坐标,在直角三角形AOC中,由OA与OC的长,利用勾股定理求出AC的长,由图形得到∠DAC为钝角,三角形ACD为等腰三角形,只有DA=AC,求出DA的长,即为m的值,即可确定出D的坐标;
(3)由P在抛物线的对称轴上,设出P坐标为(-2,n),如图所示,过O′作O′M⊥x轴,交x轴于点M,过P作PN⊥O′M,垂足为N,由旋转的性质得到一对边相等,再由同角的余角相等得到一对角相等,根据一对直角相等,利用AAS得到△PCO≌△PNO′,由全等三角形的对应边相等得到O′N=OC=2,PN=PC=|n|,再由PCMN为矩形得到MN=PC=|n|,分n大于0与小于0两种情况表示出O′坐标,将O′坐标代入抛物线解析式中求出相应n的值,即可确定出P的坐标.
![]() 将
将![]() ,
,![]() 坐标分别代入抛物线解析式得:
坐标分别代入抛物线解析式得:![]() ,
,
解得:![]() ,
,
∴抛物线解析式为![]() ,
,
∴顶点![]() 坐标为
坐标为![]() ;
;
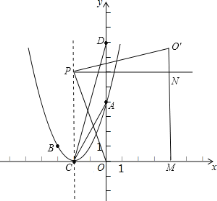
![]() 由题意得:
由题意得:![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
根据勾股定理得:![]() ,
,
由图形得到![]() 为钝角,要使
为钝角,要使![]() 为等腰三角形,只有
为等腰三角形,只有![]() ,
,
∴![]() ,
,
则![]() 坐标为
坐标为![]() ;
;
![]() 设
设![]() ,如图所示,过
,如图所示,过![]() 作
作![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,过
,过![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
易得![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵四边形![]() 为矩形,
为矩形,
∴![]() ,
,
①当![]() 时,
时,![]() ,代入抛物线解析式得:
,代入抛物线解析式得:![]() ,
,
解得:![]() 或
或![]() (舍去);
(舍去);
②当![]() 时,
时,![]() ,代入抛物线解析式得:
,代入抛物线解析式得:![]() ,
,
解得:![]() (舍去)或
(舍去)或![]() ,
,
综上①②得到![]() 或
或![]() ,
,
则![]() 的坐标为
的坐标为![]() ,
,![]() .
.

 阅读快车系列答案
阅读快车系列答案