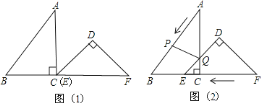题目内容
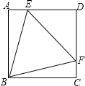
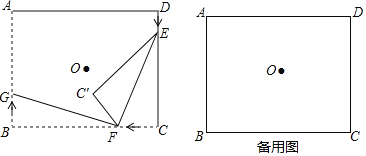
【题目】如图,点O为矩形ABCD对角线交点,![]() ,
,![]() ,点E、F、G分别从D,C,B三点同时出发,沿矩形的边DC、CB、BA匀速运动,点E的运动速度为
,点E、F、G分别从D,C,B三点同时出发,沿矩形的边DC、CB、BA匀速运动,点E的运动速度为![]() ,点F的运动速度为
,点F的运动速度为![]() ,点G的运动速度为
,点G的运动速度为![]() ,当点F到达点
,当点F到达点![]() 点F与点B重合
点F与点B重合![]() 时,三个点随之停止运动
时,三个点随之停止运动![]() 在运动过程中,
在运动过程中,![]() 关于直线EF的对称图形是
关于直线EF的对称图形是![]() 设点E、F、G运动的时间为
设点E、F、G运动的时间为![]() 单位:
单位:![]()
![]() 当
当![]() ______s时,四边形
______s时,四边形![]() 为正方形;
为正方形;
![]() 若以点E、C、F为顶点的三角形与以点F、B、G为顶点的三角形相似,求t的值;
若以点E、C、F为顶点的三角形与以点F、B、G为顶点的三角形相似,求t的值;
![]() 是否存在实数t,使得点
是否存在实数t,使得点![]() 与点O重合?若存在,直接写出t的值;若不存在,请说明理由.
与点O重合?若存在,直接写出t的值;若不存在,请说明理由.
【答案】(1)![]() (2)当
(2)当![]() 或
或![]() 时,以点E、C、F为顶点的三角形与以点F,B,G为顶点的三角形相似(3)不存在实数t,使得点
时,以点E、C、F为顶点的三角形与以点F,B,G为顶点的三角形相似(3)不存在实数t,使得点![]() 与点O重合
与点O重合
【解析】
![]() 利用正方形的性质,得到
利用正方形的性质,得到![]() ,列一元一次方程求解即可;
,列一元一次方程求解即可;
![]() 与
与![]() 相似,分两种情况,需要分类讨论,逐一分析计算;
相似,分两种情况,需要分类讨论,逐一分析计算;
![]() 本问为存在型问题
本问为存在型问题![]() 假设存在,则可以分别求出在不同条件下的t值,它们互相矛盾,所以不存在.
假设存在,则可以分别求出在不同条件下的t值,它们互相矛盾,所以不存在.
![]() 若四边形
若四边形![]() 为正方形,则
为正方形,则![]() ,
,![]() ,
,![]() ,
,
即:![]() ,
,
解得![]() ,
,
故答案为:![]() ;
;
![]() 分两种情况,讨论如下:
分两种情况,讨论如下:
![]() 若
若![]() ∽
∽![]() ,
,
则有![]() ,即
,即![]() ,
,
解得:![]() ;
;
![]() 若
若![]() ∽
∽![]() ,
,
则有![]() ,即
,即![]() ,
,
解得:![]() 不合题意,舍去
不合题意,舍去![]() 或
或![]() .
.
![]() 当
当![]() 或
或![]() 时,以点E、C、F为顶点的三角形与以点F,B,G为顶点的三角形相似.
时,以点E、C、F为顶点的三角形与以点F,B,G为顶点的三角形相似.
![]() 假设存在实数t,使得点
假设存在实数t,使得点![]() 与点O重合.
与点O重合.
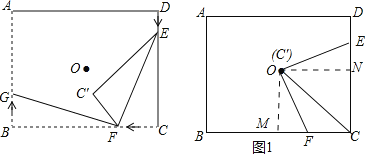
如图1,过点O作![]() 于点M,则在
于点M,则在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
由勾股定理得:![]() ,
,
即:![]()
解得:![]() ;
;
过点O作![]() 于点N,则在
于点N,则在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
由勾股定理得:![]() ,
,
即:![]()
解得:![]() .
.
![]() ,
,
![]() 不存在实数t,使得点
不存在实数t,使得点![]() 与点O重合.
与点O重合.

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案【题目】某校九年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100个)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
1号 | 2号 | 3号 | 4号 | 5号 | 总成绩 | |
甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
经统计发现两班总成绩相等,只好将数据中的其他信息作为参考.根据要求回答下列问题:
(1)计算两班的优秀率;
(2)求两班比赛数据的中位数;
(3)求两班比赛数据的方差;
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班级?简述理由.