Question

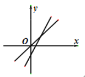
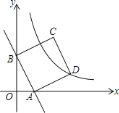
【题目】如图，在平的直角坐标系中，直线与轴、轴分别相交于点、，四边形是正方形，曲线在第一象限经过点．求双曲线表示的函数解析式．

Answer 1

【答案】．

【解析】

过点D作DE⊥x轴于点E，先由直线y=﹣2x+2与x轴，y轴相交于点A、B求出OB及OA的长，再由全等三角形的判定定理得出△AOB≌△DEA，故可得出D点坐标，再由待定系数法即可求出反比例函数的解析式．

过点D作DE⊥x轴于点E．

∵直线y=﹣2x+2与x轴，y轴相交于点A、B，∴当x=0时，y=2，即OB=2；当y=0时，x=1，即OA=1．

∵四边形ABCD是正方形，∴∠BAD=90°，AB=AD，∴∠BAO+∠DAE=90°．

∵∠ADE+∠DAE=90°，∴∠BAO=∠ADE．

∵∠AOB=∠DEA=90°，∴△AOB≌△DEA，∴DE=AO=1，AE=BO=2，∴OE=3，DE=1，∴点D的坐标为（3，1）把（3，1）代入y=中，得：k=3，故反比例函数的解析式为：y=．