题目内容
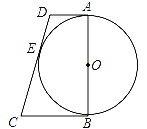
【题目】如图①，Rt△ABC中，∠B=90°，∠CAB=30°，它的顶点A的坐标为（10，0），顶点B的坐标为（5，5
），AB=10，点P从点A出发，沿A→B→C的方向匀速运动，同时点Q从点D（0，2）出发，沿y轴正方向以相同速度运动，当点P到达点C时，两点同时停止运动，设运动的时间为t秒．
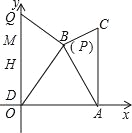
（1）当点P在AB上运动时，△OPQ的面积S（平方单位）与时间t（秒）之间的函数图象为抛物线的一部分，（如图②），则点P的运动速度为 ；
（2）求（1）中面积S与时间t之间的函数关系式及面积S的最大值及S取最大值时点P的坐标；
（3）如果点P，Q保持（1）中的速度不变，那么点P沿AB边运动时，∠OPQ的大小随着时间t的增大而增大；沿着BC边运动时，∠OPQ的大小随着时间t的增大而减小，当点P沿这两边运动时，使∠OPQ=90°的点P有 个．
【答案】（1）2个单位/秒；（2）S=
（2t+2）（10﹣t），当t=
时，S有最大值为
，此时P（
）；（3）2．
【解析】试题分析：（1）由图形可知，当点P运动了5秒时，它到达点B，此时
即可求出点P的运动速度.
过P作
轴，表示出
配方求出最大值即可.
分两种情况进行讨论即可.
试题解析：（1）由图形可知，当点P运动了5秒时，它到达点B，此时
因此点P的运动速度为10÷5=2个单位/秒，
点P的运动速度为2个单位/秒．
故答案是：2个单位/秒；
（2）如图①，过P作
轴，
∵点P的运动速度为2个单位/秒．
∴t秒钟走的路程为2t，即
∵顶点B的坐标为
∴
∴
∴
∴
又
∴
即为
中OQ边上的高，
而
可得
∴
∵
∴当
时，S有最大值为
，此时P
.
（3）当点P沿这两边运动时， 
的点P有2个．
①当点P与点A重合时， 
当点P运动到与点B重合时，OQ的长是12单位长度，
作
交y轴于点M，作
轴于点H，
由
得: 
所以
，从而
所以当点P在AB边上运动时， 
的点P有1个．
②同理当点P在BC边上运动时，可算得， 
而构成直角时交y轴于
所以
从而
的点P也有1个．
所以当点P沿这两边运动时， 
的点P有2个．
故答案是：2．
