题目内容
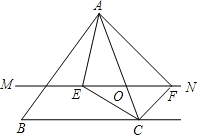
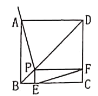
【题目】如图,点![]() 是正方形
是正方形![]() 的对角线
的对角线![]() 上一点,
上一点,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() .给出下列五个结论:①
.给出下列五个结论:①![]() ;②
;②![]() 一定是等腰直角三角形;③
一定是等腰直角三角形;③![]() 一定是等腰三角形;④
一定是等腰三角形;④![]() ;⑤
;⑤![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )
A. ①②③④B. ①②④⑤C. ②③④⑤D. ①③④⑤
【答案】B
【解析】
连接PC,根据正方形对角线的性质及题中的已知条件,证明△ABP≌△CBP后即可证明AP=PC,再根据矩形对角线相等和角的有关性质即可证明①AP=EF;④∠PFE=∠BAP;在此基础上,根据正方形的对角线平分对角的性质,在Rt△DPF中,DP2=DF2+PF2=EC2+EC2=2EC2,求得⑤DP=![]() EC,也可证明②的正确性,③只在特殊情况下成立.
EC,也可证明②的正确性,③只在特殊情况下成立.
证明:连接PC,
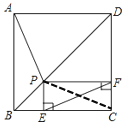
∵点P是正方形ABCD的对角线BD上一点,
∴AB=CB,∠ABP=∠CBP= 45°,BP=BP
∴△ABP≌△CBP,
∴AP=PC,∠BCP=∠BAP,
又∵![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,
∴四边形PECF是矩形,PC=EF且互相平分,
①∴AP=EF正确;∠PFE=∠FEC=∠BCP
∴④∠PFE=∠BAP正确,
③∵点P是正方形ABCD的对角线BD上任意一点,∠ADP=45°,
∴当∠PAD=45°或67.5°或90°时,△APD是等腰三角形,
除此之外,△APD不是等腰三角形,故③错误.
∵PF∥BC,
∴∠DPF=∠DBC,
又∵∠DPF=∠DBC=45°,
∴∠PDF=∠DPF=45°,即△DPF是等腰直角三角形,即②正确
∵矩形PECF中,PF=EC,
∴在等腰直角三角形△DPF中,DP2=DF2+PF2=EC2+EC2=2EC2,
∴⑤DP=![]() EC正确.
EC正确.
∴其中正确结论的序号是①②④⑤.
故选B.

【题目】为打造平安校园,增强学生安全防范意识,某校组织了全校1200名学生参加校园安全网络知识竞赛.赛后随机抽取了其中200名学生的成绩作为样本进行整理,并制作了如下不完整的频数分布表和频数分布直方图.
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | n |
60≤x<70 | 20 | 0.10 |
70≤x<80 | 30 | 0.15 |
80≤x<90 | m | 0.40 |
90≤x<100 | 60 | 0.30 |
请根据图表提供的信息,解答下列各题:
(1)表中m= ,n= ,请补全频数分布直方图.
(2)若用扇形统计图来描述成绩分布情况,则分数段80≤x<90对应扇形的圆心角的度数是 °.
(3)若成绩在80分以上(包括80分)为合格,则参加这次竞赛的1200名学生中成绩合格的大约有多少名?