题目内容
【题目】如图,现有一张边长为![]() 的正方形纸片
的正方形纸片![]() ,点
,点![]() 为正方形
为正方形![]() 边上的一点(不与点
边上的一点(不与点![]() ,点
,点![]() 重合)将正方形纸片折叠,使点
重合)将正方形纸片折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 处,点
处,点![]() 落在
落在![]() 处,
处,![]() 交
交![]() 于
于![]() ,折痕为
,折痕为![]() ,连接
,连接![]() ,
,![]() .则
.则![]() 的周长是______.
的周长是______.

【答案】16.
【解析】
解过点A作AM⊥GH于M,由正方形纸片折叠的性质得出∠EGH=∠EAB=∠ADC=90°,AE=EG,则EG⊥GH,∠EAG=∠EGA,由垂直于同一条直线的两直线平行得出AM∥EG,得出∠EGA=∠GAM,则∠EAG=∠GAM,得出AG平分∠DAM,则DG=GM,由AAS证得△ADG≌△AMG得出AD=AM=AB,由HL证得Rt△ABP≌Rt△AMP得出BP=MP,则△PGC的周长=CG+PG+PC=CG+MG+PM+PC=CG+DG+BP+PC=CD+CB=16.
解:过点A作AM⊥GH于M,如图所示:
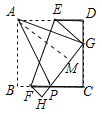
∵将正方形纸片折叠,使点A落在CD边上的G处,
∴∠EGH=∠EAB=∠ADC=90°,AE=EG,
∴EG⊥GH,∠EAG=∠EGA,
∴AM∥EG,
∴∠EGA=∠GAM,
∴∠EAG=∠GAM,
∴AG平分∠DAM,
∴DG=GM,
在△ADG和△AMG中 ,
,
∴△ADG≌△AMG(AAS),
∴AD=AM=AB,
在Rt△ABP和Rt△AMP中![]() ,
,
∴Rt△ABP≌Rt△AMP(HL),
∴BP=MP,
∴△PGC的周长=CG+PG+PC=CG+MG+PM+PC=CG+DG+BP+PC=CD+CB=8+8=16,
故答案为:16.

 初中暑期衔接系列答案
初中暑期衔接系列答案【题目】为打造平安校园,增强学生安全防范意识,某校组织了全校1200名学生参加校园安全网络知识竞赛.赛后随机抽取了其中200名学生的成绩作为样本进行整理,并制作了如下不完整的频数分布表和频数分布直方图.
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | n |
60≤x<70 | 20 | 0.10 |
70≤x<80 | 30 | 0.15 |
80≤x<90 | m | 0.40 |
90≤x<100 | 60 | 0.30 |
请根据图表提供的信息,解答下列各题:
(1)表中m= ,n= ,请补全频数分布直方图.
(2)若用扇形统计图来描述成绩分布情况,则分数段80≤x<90对应扇形的圆心角的度数是 °.
(3)若成绩在80分以上(包括80分)为合格,则参加这次竞赛的1200名学生中成绩合格的大约有多少名?






