题目内容
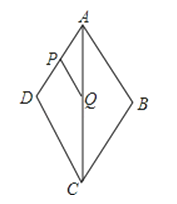
【题目】如图,AE∥BF,先按(1)的要求作图,再按(2)的要求证明
(1)用直尺和圆规作出∠ABF的平分线BD交AE于点D,连接BD,再作出BD的中点O(不写作法,保留作图痕迹)
(2)连接(1)所作图中的AO并延长与BE相交于点C,连接DC,求证:四边形ABCD是菱形.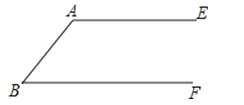
【答案】解:(1)如图.
(2)证明:∵AE∥BF,
∴∠ADO=∠CBO.
在△ADO与△CBO中, ,
,
∴△ADO≌△CBO(ASA),
∴AD=BC,
∴四边形ABCD是平行四边形.
∵BD平分∠ABC,
∴∠ABD=∠CBD.
又∵AE∥BF,
∴∠ABD=∠ADB,
∴AB=AD.
又∵点O是BD的中点,
∴AO⊥BD,即AC⊥BD.
∴平行四边形ABCD是菱形.
【解析】(1)用作一个角的角平分线和一条线段的中点的作法作图;
(2)欲证明四边形ABCD是菱形,只需推知平行四边形ABCD的对角线互相垂直即可.

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目