题目内容
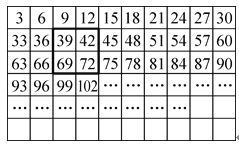
【题目】若干个3的倍数按照一定的规律排成下表,用如图所示的正方形框出四个数.
(1)如果框出的四个数的和是1158,你能确定四个数分别是多少吗?
(2)你认为能否框出四个数,使这四个数的和是190.请说明理由.
【答案】(1) 273,276,303,306.;(2) 不能
【解析】试题分析:(1)设四个数中最小的一个数是x,那么其余的三个数分别表示为x+3、x+30、x+33,根据题意列方程,求解即可;
(2)若设四个数中最小的为y,则有4y+66=190,解出y的值不是3的倍数,所以不在此数表中,因此不能框出四个数,使这四个数的和是190.
试题解析:解:(1)设四个数中最小的一个数是x,那么其余的三个数分别表示为x+3、x+30、x+33,根据题意得x+(x+3)+(x+30)+(x+33)=1158.即4x+66=1158,解得x=273.所以x+3=276,x+30=303,x+33=306,即这四个数分别是273,276,303,306.
(2)不能框出四个数,使这四个数的和是190,)理由如下:由(1)可知,若设四个数中最小的为y,则有4y+66=190,解得y=31.(10分)而31不是3的倍数,所以不在此数表中,因此不能框出四个数,使这四个数的和是190.

练习册系列答案
相关题目