Question

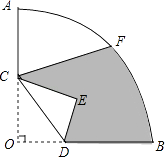
【题目】如图，在Rt△ABC中，∠ACB=90°，AC=8cm，BC=6cm，点P沿AB边从点A开始以2cm/s的速度向点B运动，点Q沿CB边从点C开始以1cm/s的速度向点B运动，P、Q同时出发，用t（s）表示运动的时间（0≤t≤5）．

（1）当t为何值时，以P、Q、B为顶点的三角形与△ABC相似．
（2）分别过点A，B作直线CP的垂线，垂足为D，E，设AD+BE=y，求y与t的函数关系式；并求当t为何值时，y有最大值．
（3）直接写出PQ中点移动的路径长度．

Answer 1

【答案】
（1）

解：∵∠ACB=90°，AC=8cm，BC=6cm，

∴BC=10cm．

由题意可知，PA=2t，BP=10﹣2t，CQ=t，BQ=6﹣t．

①若 ，则△BQP∽△BCA．

即 ．解得t=0；

②若 ，则△BQP∽△BAC．

即 ．解得t= ．

故当t=0或t= 时，以P，Q，C为顶点的三角形与△ABC相似

（2）

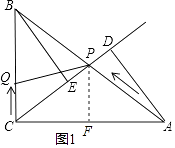
解：如图1，作PF⊥AC，垂足为F．

∴△APF∽△ABC．

∴ ，即 ，

解得PF= ，AF= ．

∴CF=8﹣ ，

∴CP= =2 ，

∵S△APC= CPAD= PFAC= 8= ，

∴AD= ．

同理BE= ．

∴y=AD+BE= + = = ，

y= = ，当t= 时，y的最大值为10cm

（3）

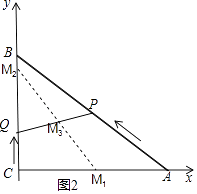
解：如图2，设PQ的中点为M，以C为原点，以AC所在直线为x轴，建立平面直角坐标系，

依题意，可知0≤t≤5，当t=0时，点M1的坐标为（4，0）；

当t=5时，点M2的坐标为（0，5.5），设直线M1M2的解析式为y=kx+b，

∴ ∴ ，

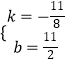∴直线M1M2的解析式为y=﹣ x+ ．

由（2）知点Q（0，t），P（8﹣ ， ），

∴在运动过程中，线段PQ中点M3的坐标为（4﹣ ， ），

把x=4﹣ ，代入y=﹣ x+ ，得y= ，

∴点M3在M1M2直线上，

∴线段PQ中点M所经过的路径长为 = cm．

【解析】（1）根据勾股定理得到BC=10，根据已知条件得到PA=2t，BP=10﹣2t，CQ=t，BQ=6﹣t．根据相似三角形的性质列方程即可得到结论；（2）如图1，作PF⊥AC，垂足为F．根据相似三角形的性质得到PF= ，AF= ．求得CF=8﹣ ，根据勾股定理得到CP= =2 ，根据三角形的面积即可得到结论；（3）如图2，设PQ的中点为M，以C为原点，以AC所在直线为x轴，建立平面直角坐标系，依题意，可知0≤t≤5，当t=0时，点M1的坐标为（4，0）；当t=5时，点M2的坐标为（0，5.5），求得直线M1M2的解析式为y=﹣ x+ ．根据勾股定理即可得到结论．
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识，掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法，以及对勾股定理的概念的理解，了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．