题目内容
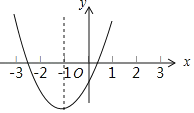
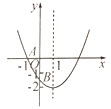
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴的交点
轴的交点![]() 在
在![]() 和
和![]() 之间(不包括这两点),对称轴为直线
之间(不包括这两点),对称轴为直线![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确的是________.
.其中正确的是________.
【答案】①③④⑤
【解析】
①由抛物线的开口方向、对称轴以及与y轴的交点,可得出a>0、b<0、c<0,进而可得出abc>0,结论①正确;②由抛物线的对称轴及点A的坐标,可得出抛物线与x轴的另一交点坐标,结合抛物线的开口可得出当x=2时,y=4a+2b+c<0,结论②错误;③由a>0、b<0、c<0,可得出![]() ,结论③正确;④由当x=-1时y=a-b+c=0,结合b=-2a可得出3a=-c,再根据-2<c<-1,即可求出
,结论③正确;④由当x=-1时y=a-b+c=0,结合b=-2a可得出3a=-c,再根据-2<c<-1,即可求出![]() ,结论④正确;⑤由a-b+c=0、a>0,可得出-b+c<0,即b>c,结论⑤正确.综上即可得出结论.
,结论④正确;⑤由a-b+c=0、a>0,可得出-b+c<0,即b>c,结论⑤正确.综上即可得出结论.
①∵抛物线开口向上,对称轴为直线x=1,与y轴的交点在(0,2)和(0,1)之间,
∴a>0, ![]() ,2<c<1,
,2<c<1,
∴b<0,abc>0,结论①正确;
②∵抛物线与x轴交于点A(1,0),对称轴为直线x=1,
∴抛物线与x轴的另一交点坐标为(3,0),
∴当x=2时,y=4a+2b+c<0,结论②错误;
③∵a>0,b<0,c<0,
∴4ac<0, ![]() >0,
>0,
∴![]() ,结论③正确;
,结论③正确;
④当x=1时,y=ab+c=0,
∴ab=c.
∵b=2a,
∴3a=c.
又∵2<c<1,
∴![]() ,结论④正确;
,结论④正确;
⑤∵当x=1时,y=ab+c=0,a>0,
∴b+c<0,
∴b>c,结论⑤正确。
综上所述:正确的结论有①③④⑤.
故答案为:①③④⑤.

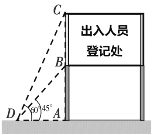
【题目】某校门口竖着“前方学校,减速慢行”的交通指示牌CD,数学“综合与实践”小组的同学将“测量交通指示牌CD的高度”作为一项课题活动,他们定好了如下测量方案:
项目 | 内容 |
课题 | 测量交通指示牌CD的高度 |
测量示意图 |
|
测量步骤 | (1)从交通指示牌下的点M处出发向前走10 米到达A处; (2)在点A处用量角仪测得∠DAM=27°; (3)从点A沿直线MA向前走10米到达B处;(4)在点B处用量角仪测得∠CBA=18°. |
请你帮助该小组同学根据上表中的测量数据,求出交通指示牌CD的高度.(参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)