Question

【题目】已知函数y＝﹣x2+bx+c（其中b，c是常数）

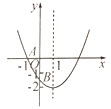
（1）四位同学在研究此函数时，甲发现当x＝0时，y＝5；乙发现函数的最大值为9；丙发现函数图象的对称轴是直线x＝2；丁发现4是方程﹣x2+bx+c＝0的一个根．已知这四位同学中只有一位发现的结论是错误的，请直接写出错误的那个人是谁，并求出此函数表达式；

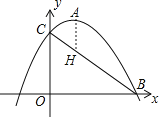
（2）在（1）的条件下，函数y＝﹣x2+bx+c的图象顶点为A，与x轴正半轴交点为B，与y轴的交点为C，若将该图象向下平移m（m＞0）个单位，使平移后得到的二次函数图象的顶点落在△ABC的内部（不包括△ABC的边界），求m的取值范围；

（3）若c＝b2，当﹣2≤x≤0时，函数y＝﹣x2+bx+c的最大值为5，求b的值．

Answer 1

【答案】（1）错误的是丁，函数的表达式为：y＝﹣x2+4x+5；（2）0＜m＜6；（3）b＝或﹣2．

【解析】

（1）假设两位同学的结论正确，用其去验证另外两个同学的结论，只要找出一个正确一个错误，即可得出结论；

（2），则点，平移后顶点坐标为：，按照平移后的图象顶点在点A、H之间求解即可；

（3）当时，写出解析式，分、、三种情况，分别求解即可．

解：（1）甲发现当时，，则；乙发现函数的最大值为9，即；

丙发现函数图象的对称轴是直线，则，即；丁发现4是方程的一个根，则，

假设甲和丙正确，即，，则即，故乙正确，而丁错误，

故错误的是丁，函数的表达式为：；

（2），则点，平移后顶点坐标为：，

，令，则或，故点，而点，

过点A作y轴的平行线交BC于点H，

由点B、C的坐标得，直线BC的表达式为：，

当时，，故点，

函数图象的顶点落在的内部，则，

解得：；

（3），则抛物线的表达式为：，函数的对称轴为：，

当时，即，

则时，y取得最大值，即，解得：舍去负值；

当时，即，

当时，y取得最大值，即，解得：舍去；

当时，

则时，y取得最大值，即，解得： （不合题意舍去；

综上，或．