Question

【题目】如图，在菱形ABCD中，∠ABC与∠BAD的度数比为1：2，周长是40cm．求：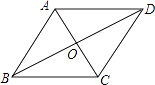

（1）两条对角线AC、BD的长度；
（2）菱形ABCD的面积．

Answer 1

【答案】
（1）解：∵四边形ABCD是菱形，

∴AB=BC，AC⊥BD，AD∥BC，

∴∠ABC+∠BAD=180°，

∵∠ABC与∠BAD的度数比为1：2，

∴∠ABC= ×180°=60°，

∴∠ABO= ∠ABC=30°，

∵菱形ABCD的周长是40cm．

∴AB=10cm，

∴OA= AB=5cm，

∴OB= =5 ，

∴AC=2OA=10cm，BD=2OB=10 cm

（2）解：S菱形ABCD= ACBD= ×10×10 =50 （cm2）
【解析】（1）由在菱形ABCD中，∠ABC与∠BAD的度数比为1：2，周长是40cm，可求得△ABO是含30°角的直角三角形，AB=10cm，继而求得AC与BD的长；（2）由菱形的面积等于其对角线积的一半，即可求得答案．
【考点精析】通过灵活运用菱形的性质，掌握菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半即可以解答此题．