题目内容
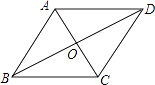
【题目】直角三角板ABC中,∠A=30°,BC=1.将其绕直角顶点C逆时针旋转一个角![]() (
(![]() 且
且![]() ),得到Rt△
),得到Rt△![]() .
.
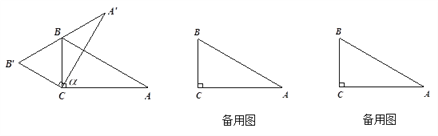
(1)如图,当边![]() 经过点B时,求旋转角
经过点B时,求旋转角![]() 的度数;
的度数;
(2)在三角板旋转的过程中,边![]() 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥![]() 交
交![]() 边于点E,联结BE.
边于点E,联结BE.
①当![]() 时,设AD=
时,设AD=![]() ,BE=
,BE=![]() ,求
,求![]() 与
与![]() 之间的函数解析式及自变量
之间的函数解析式及自变量![]() 的取值范围;
的取值范围;
②当![]() 时,求AD的长.
时,求AD的长.
【答案】(1)![]() =
=![]() ;(2)①
;(2)① ![]() (0﹤
(0﹤![]() ﹤2);②AD=1或
﹤2);②AD=1或![]() .
.
【解析】(1)由旋转的性质可得出∠α=∠B′CB=60°;
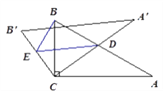
(2)①当0°<α<90°时,点D在AB边上(如图).根据平行线DE∥A'B'分线段成比例知![]() 、及由旋转性质可知,CA=CA',CB=CB',∠ACD=∠BCE由此证明△CAD∽△CBE;根据相似三角形的对应边成比例、直角三角形的性质及∠A=30°求得y=
、及由旋转性质可知,CA=CA',CB=CB',∠ACD=∠BCE由此证明△CAD∽△CBE;根据相似三角形的对应边成比例、直角三角形的性质及∠A=30°求得y=![]() x(0<x<2);
x(0<x<2);
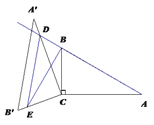
②先求得△ABC的面积,再由△CAD∽△CBE,求得BE,分情况讨论:当点D在AB边上时,AD=x,BD=AB-AD=2-x;当点D在AB的延长线上时,AD=x,BD=x-2.
解:(1)在Rt△![]() 中,∵∠A=30°,∴
中,∵∠A=30°,∴![]() .
.
由旋转可知:![]() ,
,![]() ,
,![]()
∴△![]() 为等边三角形.
为等边三角形.
∴![]() =
=![]() .
.
(2)① 当![]() 时,点D在AB边上(如图).
时,点D在AB边上(如图).
∵ DE∥![]() ,∴
,∴ ![]() .
.
由旋转性质可知,CA =![]() ,CB=
,CB=![]() , ∠ACD=∠BCE.
, ∠ACD=∠BCE.
∴ ![]() ∴
∴ ![]() .
.
∴ △CAD∽△CBE.
∴![]() .∵∠A=30° ∴
.∵∠A=30° ∴![]()
![]() .
.
∴![]() (0﹤
(0﹤![]() ﹤2)
﹤2)
②当![]() 时,点D在AB边上
时,点D在AB边上
AD=x,![]() ,∠DBE=90°.
,∠DBE=90°.
此时,![]() .
.
当S =![]() 时,
时,![]() .整理,得
.整理,得 ![]() .
.
解得 ![]() ,即AD=1.
,即AD=1.
当![]() 时,点D在AB的延长线上(如图).
时,点D在AB的延长线上(如图).
仍设AD=x,则![]() ,∠DBE=90°.
,∠DBE=90°.
![]() .
.
当S =![]() 时,
时,![]() .
.
整理,得 ![]() .
.
解得 ![]() ,
,![]() (负值,舍去).
(负值,舍去).
即![]() .
.
综上所述:AD=1或![]() .
.
“点睛”本题主要考查旋转、全等三角形、解直角三角形、平行线分线段成比例等知识.解决本题的关键是结合图形,分类讨论.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案