Question

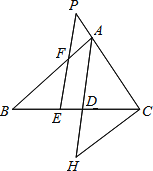
【题目】在△ABC中，AD平分∠BAC，E是BC上一点，BE＝CD，EF∥AD交AB于F点，交CA的延长线于P，CH∥AB交AD的延长线于点H，

①求证：△APF是等腰三角形；

②猜想AB与PC的大小有什么关系？证明你的猜想．

Answer 1

【答案】①证明见解析；②AB＝PC．

【解析】

①根据题意作出图形，根据两直线平行，内错角相等可得∠1＝∠4，同位角相等可得∠2＝∠P，再根据角平分线的定义可得∠1＝∠2，然后求出∠4＝∠P，根据等角对等边的性质即可得证；

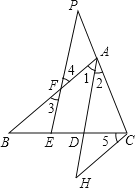
②根据两直线平行，内错角相等可得∠5＝∠B，再求出∠H＝∠1＝∠3，然后利用“AAS”证明△BEF和△CDH全等，根据全等三角形对应边相等可得BF＝CH，再求出AC＝CH，再根据AB＝AF+BF，PC＝AP+AC，整理即可得解．

①证明：∵EF∥AD，

∴∠1＝∠4，∠2＝∠P，

∵AD平分∠BAC，

∴∠1＝∠2，

∴∠4＝∠P，

∴AF＝AP，

即△APF是等腰三角形；

②AB＝PC．理由如下：

证明：∵CH∥AB，

∴∠5＝∠B，∠H＝∠1，

∵EF∥AD，

∴∠1＝∠3，

∴∠H＝∠3，

在△BEF和△CDH中，

∵，

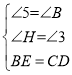∴△BEF≌△CDH（AAS），

∴BF＝CH，

∵AD平分∠BAC，

∴∠1＝∠2，

∴∠2＝∠H，

∴AC＝CH，

∴AC＝BF，

∵AB＝AF+BF，PC＝AP+AC，

∴AB＝PC．