Question

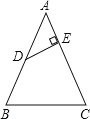
【题目】如图，四边形ABCD中，AB∥CD，AB⊥BC，AB＝BC，AB＞CD，AE⊥BD于E交BC于F.

(1)若AB＝2CD；

①求证：BC＝2BF；

②连CE，若DE＝6，CE＝，求EF的长；

(2)若AB＝6，则CE的最小值为______.

Answer 1

【答案】(1)①见解析；②EF=2；(2) .

【解析】

（1）①证明△ABF≌△BCD（ASA），得出BF=CD，由已知AB=2CD，AB=BC，即可得出BC=2BF；
②设EF=x,证明△BEF∽△BCD，得出，用x依次表示出BE、BF、BC、CD、BD,然后根据6+BE=BD列出方程，解方程即可；

（2）取AB的中点O，连接OE，由直角三角形斜边上的中线性质得出OE= AB=3，当O、E、C三点共线时，OE+CE最短，此时CE最短.由勾股定理得出，即可得出答案．

（1）①证明：∵AB∥CD，AB⊥BC，
∴BC⊥CD，∠ABF=90°，∠BAF+∠BFE=90°，
∴∠BCD=90°，
∵AE⊥BD，
∴∠BEF=90°，
∴∠BFE+∠CBD=90°，
∴∠BAF=∠CBD，
在△ABF和△BCD中，

，

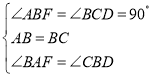∴△ABF≌△BCD（ASA），
∴BF=CD，
∵AB=2CD，AB=BC，
∴BC=2BF；
②解：∵∠BEF=∠BCD=90°，∠EBF=∠CBF，
∴△BEF∽△BCD，

，

∴，

∴设EF=x,则BE=2x，

∴BF= ，

∴BC= 2，CD=，

∴BD= ,

∴6+2x=5x,

∴x=2,

∴EF=2；
（2）解：如图2所示：取AB的中点O，连接OE，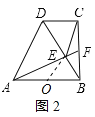

∵∠AEB=90°，AB=6,
∴OE=AB=3，
当O、E、C三点共线时，OE+CE最短，此时CE最短，

∵BC=AB=6，∠ABC=90°，
∴OC=

∴CE的最小值=OC-OE=

故答案为：