题目内容
【题目】如图,△ABC为等边三角形,过点B作BD⊥AC于点D,过D作DE∥BC,且DE=CD,连接CE, 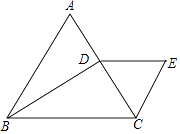
(1)求证:△CDE为等边三角形;
(2)请连接BE,若AB=4,求BE的长.
【答案】
(1)解:∵△ABC为等边三角形,
∴∠ACB=60°,
∵DE∥BC,
∴∠EDC=∠ACB=60°,
又∵DE=DC,
∴△CDE为等边三角形;
(2)解:过点E作EH⊥BC于H,

∵BD⊥AC,
∴CD= ![]() AC=
AC= ![]() AB=2,
AB=2,
又∵△CDE为等边三角形,
∴CE=CD=2,
∵∠ECH=60°,
∴EH=ECsin60°=2× ![]() =
= ![]() ,CH=ECcos60°=1,
,CH=ECcos60°=1,
∴ ![]() .
.
【解析】(1)根据∠EDC=60°,DE=DC,运用有一个角是60°的等腰三角形是等边三角形进行判断即可.(2)过点E作EH⊥BC于H,构造直角三角形,先求得EH=ECsin60°=2× ![]() =
= ![]() ,CH=ECcos60°=1,进而得到
,CH=ECcos60°=1,进而得到 ![]() .
.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目