��Ŀ����
����Ŀ�����壺�����������һ���ϵ����߳�ǡ�õ�����ߵij�����ô�����������Ϊ���������������������߳�Ϊ�������������������߳�Ϊ��������������
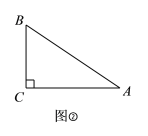
���⣺��1��������ͼ���л�һ����ABΪ�����ߵĺ��������Σ�ʹ����������C���ڸ���ϣ�
 ����������
����������
��2����ͼ�ڣ���Rt��ABC�У���C=90����![]() ����֤����ABC������������������
����֤����ABC������������������
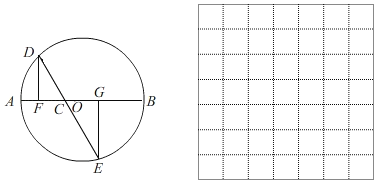
���ã���3����֪��������ABC������������������AB=AC=20����ױ�BC�ij�����ͼ��𣩣�
���𰸡���1����ͼ������������2������������3���ױ�BC�ij�Ϊ![]() ��
��![]() ��
��
��������
��1���������������������Ķ��廭��ͼ�μ��ɣ�
��2����ͼ�ڣ����ݶ���Rt��ABC�У���������һ���ǽϳ�ֱ�DZ��ϵ����ߣ��������������������Ķ���֤�����ɣ�
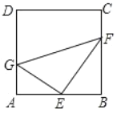
��3���������������ͼ�ۣ������ϵ�����BD=ACʱ����AB=BD����B��BE��AD��E����ͼ�ܣ����ױ��ϵ�����AD=BCʱ����AD��BC����AD=2BD���ֱ���⼴�ɽ�����⣮
��1����ͼ��

��2��֤������ͼ�ڣ�
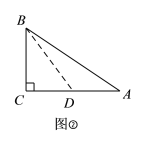
���ݶ��壬
Rt��ABC��
��������һ���ǽϳ�ֱ�DZ��ϵ����ߣ�
ȡAC���е�D������BD��
��AC��2x����CD��AD��x��
��![]() ��
��![]() ��
��
��![]() ��
��
��Rt��BCD��
![]()
��BD��AC��
���ABC������������������
��3�������������
��ͼ�ۣ������ϵ�����BD=ACʱ����AB=BD����B��BE��AD��E��
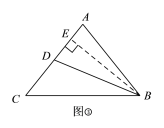
��AB=AC=20��
��BD=20��
![]() ��
��
��CE=10+5=15��
��Rt��BDE��![]() ��
��
��Rt��BCE��
![]() ��
��
��ͼ�ܣ����ױ��ϵ�����AD=BCʱ����AD��BC����AD=2BD��
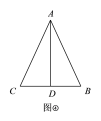
��BD=x��
��![]() ��
��
��![]() ��
��
�֡�x��0����![]() ��
��
��![]() ��
��
�����������ױ�BC�ij�Ϊ![]() ��
��![]() ��
��

 ѧ���쳵��������������������ϵ�д�
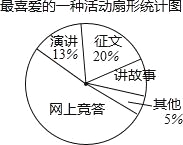
ѧ���쳵��������������������ϵ�д�����Ŀ�����ڣ�������Сѧ�㷺��չ�ˡ������л��Ļ�������������������������������ij��ѧΪ�˽�ѧ����ϲ���Ļ��ʽ���ԡ�����ϲ����һ�ֻ��Ϊ���⣬��������������飬�ռ������������Ƴ�����������������ͳ��ͼ���������ͼ���ṩ����Ϣ�������������⣺
��ϲ����һ�ֻͳ�Ʊ�
���ʽ | ���� | ������ | �ݽ� | ���Ͼ��� | ���� |
���� | 60 | 30 | 39 | a | b |
��1������γ��������У�һ�������˶�����ѧ��������ͳ��ͼ�С������¡����ֵ�Բ�Ľ��Ƕ��ٶȣ�
��2�����������ѧ����ѧ��3800������ô���������ϲ�����Ļ��ѧ��������
����Ŀ����ͼ��AB����O��ֱ����AB=4cm��CΪAB��һ���㣬����C��ֱ�߽���O��D��E���㣬�ҡ�ACD=60�㣬DF��AB�ڵ�F��EG��AB�ڵ�G������C��AB���˶�ʱ����AF=xcm��DE=ycm(��x��ֵΪ0��3ʱ��y��ֵΪ2)��̽������y���Ա���x�ı仯���仯�Ĺ��ɣ�
��1��ͨ��ȡ�㡢��ͼ���������õ���x��y�ļ����Ӧֵ�����±���
x/cm | 0 | 0.40 | 0.55 | 1.00 | 1.80 | 2.29 | 2.61 | 3 |
y/cm | 2 | 3.68 | 3.84 | 3.65 | 3.13 | 2.70 | 2 |
��2������ƽ��ֱ������ϵ������Բ�ȫ��ı��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ��
��3����ϻ����ĺ���ͼ������⣺��F���O�غ�ʱ��DE����ԼΪ��������cm(�������һλС��)��