题目内容
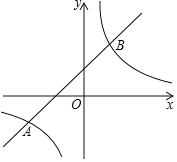
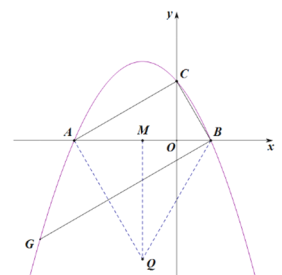
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,OB=1,∠OBC=60°.
与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,OB=1,∠OBC=60°.
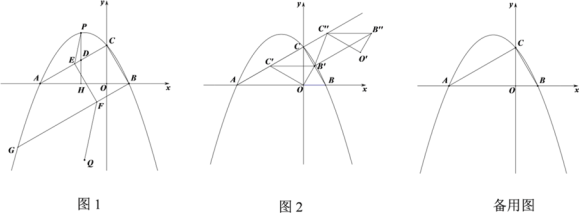
(1)如图1,求直线BC的解析式;
(2)如图1,线段AC上方抛物线上有一动点P,PD⊥x轴于点H,交线段AC于点D,直线BG∥AC,交抛物线于点G,点F是直线BC上一动点,FE∥BC交AC于点E,点Q是点A关于直线BG的对称点,连接PE、QF.当线段PD取最大值时,求PE+EF+QF的最小值及点E的坐标;
(3)如图2,将△BOC绕点O逆时针旋转至△B′O C′的位置,点B、C的对应点分别为点B′、C′,点B′恰好落在BC上.将△B′O C′沿直线AC平移,得到△B′′O ′ C′′,点B′、C′、O的对应点分别为点B′′、C′′、O ′,连接B ′ B′′、B ′C′′,△B ′B′′C′′是否能为等腰三角形?若能,请直接写出所有符合条件的C′′的坐标;若不能,请说明理由.
【答案】(1)![]() ;(2)PE+EF+QF最小值为
;(2)PE+EF+QF最小值为 ![]() +2, E点坐标
+2, E点坐标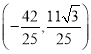 ;(3)能,
;(3)能,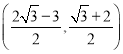 ,
,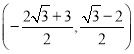 ,
,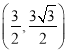 ,
,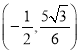
【解析】
(1)利用三角函数求出OC的长得到抛物线的解析式,求出图象与x轴的交点,设直线BC解析式为:![]() ,即可将点B、C的坐标代入求出答案;
,即可将点B、C的坐标代入求出答案;
(2)先求出直线AC的解析式,设点P、D的坐标,根据PD最大求得点P的坐标,利用勾股定理的逆定理及对称性得到△ABQ是等边三角形,过点Q作QM⊥x轴于点M,求出点Q的坐标,根据平移规律得到Q ′的坐标,连接P Q ′交AC于点E,再利用勾股定理求出![]() , 得到PE+EF+QF最小值= P Q ′+EF,由此求出答案;
, 得到PE+EF+QF最小值= P Q ′+EF,由此求出答案;
(3)根据点的位置分四种情况进行求解:①当![]() =
=![]() 时,②当
时,②当![]() =
=![]() 时,③当
时,③当![]() 时,④当
时,④当![]() 时,分别求出点C′′的坐标.
时,分别求出点C′′的坐标.
(1)在△BOC 中,OB=1,∠OBC=60°
∴BC=2,OC=![]() ,
,
∴抛物线解析式为:![]()
令y=0,得![]() ,
,
解之得![]() ,
,![]() ,
,
∴A(-3,0),B(1,0),C(0,![]() ),
),
设直线BC解析式为:![]() ,经过B(1,0),C(0,
,经过B(1,0),C(0,![]() ),
),
∴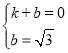 ,
,
得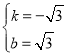 ,
,
∴![]() ;
;
(2)设直线AC解析式为:![]() ,经过A(-3,0),B(1,0),得
,经过A(-3,0),B(1,0),得![]() ,
,
设P点坐标为![]() ,则D点坐标为
,则D点坐标为![]() ,
,
∴PD=![]()
![]()
当![]() 时,PD有最大值,
时,PD有最大值,
∴P点坐标为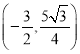 ,
,
在R△AOC中,可以求出AC=2![]() ,AB=4 ,
,AB=4 ,
∴AC2+BC2=12+4=16=AB2
由勾股定理逆定理得,可得∠ACB=90°,
可得∠CAB=30°=∠ABG,
由对称可得,AB=BQ=4, ∠ABQ=30°+30°=60°,
∴△ABQ是等边三角形,
过点Q作QM⊥x轴于点M,
∴MB=4,且OB=1
∴OM=1,QM=2![]()
∴Q点坐标为(-1,-2![]() )
)
由题意得,四边形BCEF是矩形,可得EF=BC=2,
将Q点沿射线EF方向平移2个单位(向左平移1个单位,向上平移![]() 个单位),可得Q ′的坐标为(-2,-
个单位),可得Q ′的坐标为(-2,-![]() )
)
连接P Q ′交AC于点E,点E即为所求,
P Q ′=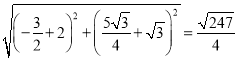
PE+EF+QF最小值= P Q ′+EF= ![]() +2,
+2,
直线P Q的解析式为:![]()
联立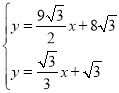 ,可得E点坐标
,可得E点坐标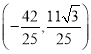
(3)存在,
∵A(-3,0),B(1,0),C(0,![]() ),
),
∴OA=3,OB=1,OC=![]() ,
,
∴![]() ,
,![]() ,
,
∴∠ACB=90°,
∴∠CAB=30°,AC=2![]() ,
,
∴,![]()
由旋转得到![]() ,
, ![]() ,
,
∵![]() ∥
∥![]() ,
,![]() =
=![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
①将三角形向上平移,当![]() =
=![]() 时,如图1,延长
时,如图1,延长![]() 交y轴于D,
交y轴于D,
∴四边形![]() 是菱形,
是菱形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴OD=OC+CD=![]() ,
,
∴![]()
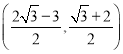 ;
;
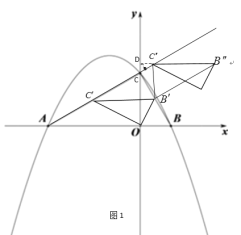
②将三角形向下平移,当![]() =
=![]() 时,如图2,则四边形
时,如图2,则四边形![]() 是菱形,
是菱形,
∴![]()
过点![]() 作
作![]() ⊥
⊥![]() ,
,
∵![]() ,
,
∴![]() =1,
=1,![]() ,
,
∴点![]() 的横坐标是
的横坐标是![]() ,纵坐标是
,纵坐标是![]() ,
,
∴点![]() 的坐标是
的坐标是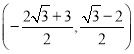 ;
;
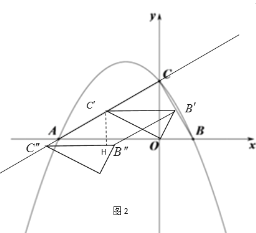
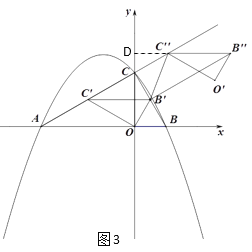
③当![]() 时,如图3,
时,如图3,
则![]() ,
,
∵∠ACB=90°,
∴![]() ,
,
延长![]() 交y轴于D,
交y轴于D,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴OD=OC+CD=![]() ,
,
∴点![]() 的坐标是
的坐标是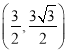 ;
;
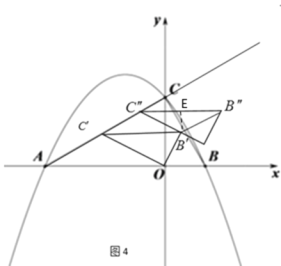
④当![]() 时,如图4,过点
时,如图4,过点![]() 作
作![]() ⊥
⊥![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() 的横坐标是
的横坐标是![]() ,纵坐标是
,纵坐标是![]() ,
,
∴点![]() 的坐标是
的坐标是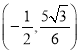 ,
,
综上,点![]() 的坐标是
的坐标是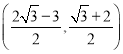 ,
,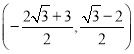 ,
,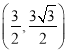 ,
,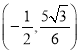 .
.

 特高级教师点拨系列答案
特高级教师点拨系列答案