题目内容
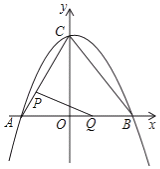
【题目】如图,在平面直角坐标系中,二次函数y=﹣![]() x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
(1)求二次函数的解析式;
(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;
(3)点M在抛物线上,且△AOM的面积与△AOC的面积相等,求出点M的坐标.
【答案】(1)y=﹣![]() x2+
x2+![]() x+4;(2)在点P,Q运动过程中,△APQ不可能是直角三角形,理由详见解析;(3)M(1,4)或(
x+4;(2)在点P,Q运动过程中,△APQ不可能是直角三角形,理由详见解析;(3)M(1,4)或(![]() ,﹣4)或(
,﹣4)或(![]() ,﹣4).
,﹣4).
【解析】
(1)判断出抛物线的解析式中二次项系数,再利用交点式,即可得出结论;
(2)分两种情况:当∠AQP=90°,判断出点P在y轴右侧,不符合题意,当∠APQ=90°时,根据相似三角形的性质得出比例式,建立方程求出t的值,而t大于4,也不符合题意,即可得出结论;
(3)先求出△AOC的面积,进而得出△AOM的面积,进而建立方程求解即可得出结论.
解:(1)∵二次函数y=﹣![]() x2+bx+c过点A(﹣3,0),B(4,0),
x2+bx+c过点A(﹣3,0),B(4,0),
∴抛物线的解析式为y=﹣![]() (x+3)(x﹣4)=﹣
(x+3)(x﹣4)=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)在点P,Q运动过程中,△APQ不可能是直角三角形,
理由:由(1)知,抛物线的解析式为y=﹣![]() x2+
x2+![]() x+4,
x+4,
∴C(0,4),
∵A(﹣3,0),B(4,0),
∴AC=5,OA=3,OC=4,
由运动知,AP=t,OQ=t,
∴AQ=3+t,(0<t<4)
∵∠OAP是Rt△AOC的一个锐角,
∵△APQ是直角三角形,
①当∠AQP=90°时,
∵∠AOC=90°=∠AQP,
∴PQ∥y轴,
∵点Q在OB上,
∴点P不可能在第二象限内,此种情况不存在,
②当∠APQ=90°时,
∵∠AOC=90°=∠APQ,
∵∠PAQ=∠OAC,
∴△AOC∽△APQ,
∴![]() ,
,
∴![]() ,
,
∴t=![]() ,
,
∵0<t<4,
∴此种情况不符合题意,
即在点P,Q运动过程中,△APQ不可能是直角三角形;
(3)由(2)知,OA=3,OC=4,
∴S△AOC=![]() OAOC=6,
OAOC=6,
∵△AOM的面积与△AOC的面积相等,
∴S△AOM=6,
设点M(m,﹣![]() m2+
m2+![]() m+4),
m+4),
∴S△AOM=![]() OA|﹣
OA|﹣![]() m2+
m2+![]() m+4|=
m+4|=![]() |﹣
|﹣![]() m2+
m2+![]() m+4|=6,
m+4|=6,
∴m=0(舍)或m=1或![]() ,
,
∴M(1,4)或(![]() ,﹣4)或(
,﹣4)或(![]() ,﹣4).
,﹣4).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某商场的运动服装专柜,对![]() 两种品牌的远动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表.
两种品牌的远动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表.
第一次 | 第二次 | |
| 20 | 30 |
| 30 | 40 |
累计采购款/元 | 10200 | 14400 |
(1)问![]() 两种品牌运动服的进货单价各是多少元?
两种品牌运动服的进货单价各是多少元?
(2)由于![]() 品牌运动服的销量明显好于
品牌运动服的销量明显好于![]() 品牌,商家决定采购
品牌,商家决定采购![]() 品牌的件数比
品牌的件数比![]() 品牌件数的
品牌件数的![]() 倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件
倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件![]() 品牌运动服?
品牌运动服?