题目内容
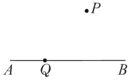
【题目】如图,在平面内。点![]() 为线段
为线段![]() 上任意一点.对于该平面内任意的点
上任意一点.对于该平面内任意的点![]() ,若满足
,若满足![]() 小于等于
小于等于![]() 则称点
则称点![]() 为线段
为线段![]() 的“限距点”.
的“限距点”.
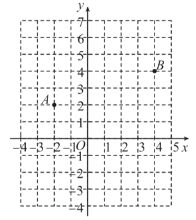
(1)在平面直角坐标系![]() 中,若点
中,若点![]() .
.
①在的点![]() 中,是线段
中,是线段![]() 的“限距点”的是 ;
的“限距点”的是 ;
②点P是直线![]() 上一点,若点P是线段AB的“限距点”,请求出点P横坐标
上一点,若点P是线段AB的“限距点”,请求出点P横坐标![]() 的取值范围.
的取值范围.
(2)在平面直角坐标系![]() 中,若点
中,若点![]() .若直线
.若直线![]() 上存在线段AB的“限距点”,请直接写出
上存在线段AB的“限距点”,请直接写出![]() 的取值范围
的取值范围
【答案】(1)①E;②![]() ;(2)
;(2)![]() .
.
【解析】
(1)①分别计算出C、D、E到A、B的距离,根据“限距点”的含义即可判定;
②画出图形,由“限距点”的定义可知,当点P位于直线![]() 上x轴上方并且AP
上x轴上方并且AP![]() 时,点P是线段AB的“限距点”,据此可解;
时,点P是线段AB的“限距点”,据此可解;
(2)画出图形,可知当![]() 时,直线
时,直线![]() 上存在线段AB的“限距点”,据此可解.
上存在线段AB的“限距点”,据此可解.
(1)①计算可知AC=BC= ![]() ,DA=
,DA= ![]() ,DB=
,DB= ![]() ,EA=EB=2,
,EA=EB=2,
设点![]() 为线段
为线段![]() 上任意一点,则
上任意一点,则
![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
∴点E为线段AB的“限距点”.
故答案是:E.
②如图,作PF⊥x轴于F,
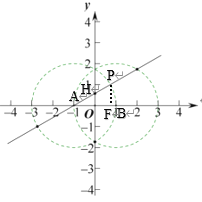
由“限距点”的定义可知,当点P位于直线![]() 上x轴上方并且AP
上x轴上方并且AP![]() 时,点P是线段AB的“限距点”,
时,点P是线段AB的“限距点”,
∵直线![]() 与x轴交于点A(-1,0),交y轴于点H(0,
与x轴交于点A(-1,0),交y轴于点H(0,![]() ),
),
∴∠OAH=30°,
∴当AP=2时,AF=![]() ,
,
∴此时点P的横坐标为![]() -1,
-1,
∴点P横坐标![]() 的取值范围是
的取值范围是 ![]() ;
;
(2)如图,直线![]() 与x轴交于M,AB交x轴于G,
与x轴交于M,AB交x轴于G,
∵点A(t,1)、B(t,-1),
直线![]() 与x轴的交点M(-1,0),与y轴的交点C(0,
与x轴的交点M(-1,0),与y轴的交点C(0,![]() ),
),
∴![]() ,
,
∴∠NMO=30°,
①当圆B与直线![]() 相切于点N,连接BN,连接BA并延长与直线
相切于点N,连接BN,连接BA并延长与直线![]() 交于D(t,
交于D(t,![]() )点,
)点,
∵∠NBD=∠NMO=30°,
∴![]() ,
,
即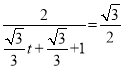 ,
,
解得:![]() ;
;
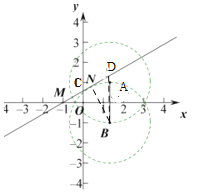
②当圆A与直线![]() 相切时,
相切时,
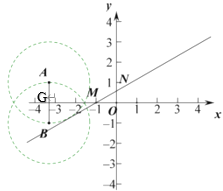
同理可知:![]()
∴![]() .
.

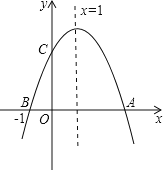
【题目】抛物线![]() 中,函数值y与自变量
中,函数值y与自变量![]() 之间的部分对应关系如下表:
之间的部分对应关系如下表:
| … |
|
|
| 0 | 1 | … |
y | … |
|
| 0 |
|
| … |
(1)求该抛物线的表达式;
(2)如果将该抛物线平移,使它的顶点移到点M(2,4)的位置,那么其平移的方法是____________.