题目内容
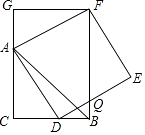
【题目】如图1,已知正方形ABCD的边长为5,点E在边AB上,AE=3,延长DA至点F,使AF=AE,连结EF.将△AEF绕点A顺时针旋转![]() (0°<
(0°<![]() <90°),如图2所示,连结DE、BF.
<90°),如图2所示,连结DE、BF.
(1)请直接写出DE的取值范围:_______________________;
(2)试探究DE与BF的数量关系和位置关系,并说明理由;
(3)当DE=4时,求四边形EBCD的面积.

【答案】(1)DE的取值范围:2<DE<![]() ;(2)DE=BF,DE⊥BF,理由详见解析;(3)当DE=4时,四边形EBCD的面积为14.5.
;(2)DE=BF,DE⊥BF,理由详见解析;(3)当DE=4时,四边形EBCD的面积为14.5.
【解析】
(1)根据点E在AB边上和在AD边上时DE分别为最大值和最小值解答即可;(2)延长DE,交AB于点G,交BF于点H,易得∠EAD=∠FAB,根据SAS可证明△EAD≌△FAB,即可得DE=BF,∠ADE=∠ABF,根据∠AGD=∠BGH,∠ADE+∠AGD=90°可得∠ABF+∠BGH=90°进而可得∠BHG=90° 即DE⊥BF;(3)由AE=3,DE=4,AD=5可得△AED是直角三角形,由(2)得△EAD≌△FAB,可知∠AFB=∠AED=90°,BF=DE=4,![]() ,由∠EAF=90°可得AE//BF,进而可求出四边形ABEF得面积,根据
,由∠EAF=90°可得AE//BF,进而可求出四边形ABEF得面积,根据![]()
![]() 即可得答案.
即可得答案.
(1)∵点E在AB边上和在AD边上时DE分别为最大值和最小值,
∴![]() ,5-3=2,
,5-3=2,
∴DE的取值范围:2<DE<![]() ;
;
(2)DE=BF,DE⊥BF,理由如下:
延长DE,交AB于点G,交BF于点H
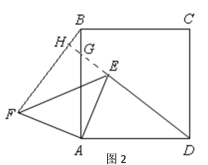
∵∠BAD=∠FAE=90°
即∠BAE+∠EAD=∠BAE+∠FAB=90°
∴∠EAD=∠FAB
在△EAD和△FAB中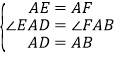
∴△EAD≌△FAB
∴DE=BF,∠ADE=∠ABF
又∵∠AGD=∠BGH,∠ADE+∠AGD=90°
∴∠ABF+∠BGH=90°
∴∠BHG=90° 即DE⊥BF
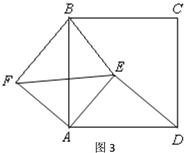
(3)∵AE=3,DE=4,AD=5
∴![]()
∴△ADE为直角三角形,∠AED=90°
由(2)得△EAD≌△FAB
∴∠AFB=∠AED=90°,BF=DE=4,![]()
又∵∠EAF=90°
∴AE∥BF
∴四边形AEBF的面积为:![]() =
=![]() =10.5
=10.5
∴![]() =10.5
=10.5
∴![]()
![]() 52-10.5=14.5
52-10.5=14.5
答:当DE=4时,四边形EBCD的面积为14.5.