题目内容
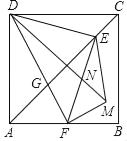
【题目】小清为班级办黑板报时遇到一个难题,在版面设计过程中需要将一个半圆三等分,小华帮他设计了一个尺规作图的方法.
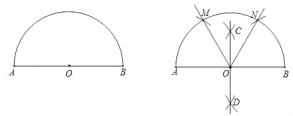
小华的作法如下:
(1)作AB的垂直平分线CD交AB于点O;
(2)分别,以A、B为圆心,以AO(或BO)的长为半径画弧,分别交半圆于点M、N;
(3)连接OM、ON即可
请根据该同学的作图方法完成以下推理:
∵半圆AB
∴ 是直径.
∵CD是线段AB的垂直平分线
∴OA=OB(依据: )
∵OA=OM=
∴△OAM为等边三角形(依据: )
∴∠AOM=60°(依据: )
同理可得∠BON=60°
∠AOM=∠BON=∠MON=60°
【答案】AB,中垂线的定义,AM,等边三角形的定义,等边三角形的性质.
【解析】
应先做线段AB的垂直平分线,得到半圆的圆心;三等分平角,那么平分而成的每个角是60°根据半径相等,可得到相邻两个半径的端点与圆心组成一个等边三角形.以A为圆心,半径长为半径画弧,就可得到一个另一半径的端点所在的位置,连接它与圆心,就得到一条三等分线,同法做到另一三等分线.
解:∵半圆AB,
∴AB是直径.
∵CD是线段AB的垂直平分线
∴OA=OB(依据:中垂线的定义)
∵OA=OM=AM,
∴△OAM为等边三角形(依据:等边三角形的定义)
∴∠AOM=60°(依据:等边三角形的性质)
同理可得∠BON=60°
∠AOM=∠BON=∠MON=60°,
故答案为:AB,中垂线的定义,AM,等边三角形的定义,等边三角形的性质.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目