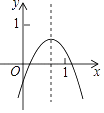题目内容
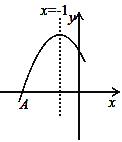
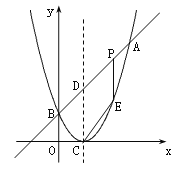
【题目】如图,已知二次函数图象的顶点坐标为C(1,0),直线![]() 与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴
与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴![]() 上.
上.
(1)求![]() 的值及这个二次函数的关系式;
的值及这个二次函数的关系式;
(2)P为线段AB上的一个动点(点P与A、B不重合),过P作![]() 轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为
轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为![]() ,点P的横坐标为
,点P的横坐标为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,P点坐标为(2,3).
;(3)存在,P点坐标为(2,3).
【解析】
试题(1)、将点A代入直线解析式求出m的值,将二次函数设出顶点式,然后求出函数解析式;(2)、分别得出点P和点E的纵坐标,然后将两点的纵坐标做差得出h与x的函数关系式;(3)、根据平行四边形性质可得:PE=DC,根据点D在直线y=x+1上得出点D的坐标,从而得出方程求出x的值,得出点P的坐标.
试题解析:(1)、∵点A(3,4)在直线y=x+m上,∴4=3+m. ∴m=1.
设所求二次函数的关系式为y=a(x-1)2. ∵点A(3,4)在二次函数y=a(x-1)2的图象上,
∴4=a(3-1)2, ∴a=1. ∴所求二次函数的关系式为y=(x-1)2.即y=x2-2x+1.
(2)、设P、E两点的纵坐标分别为yP和yE∴PE=h=yP-yE=(x+1)-(x2-2x+1)=-x2+3x.
即h=-x2+3x(0<x<3).
(3)、存在.要使四边形DCEP是平行四边形,必需有PE=DC.∵点D在直线y=x+1上,
∴点D的坐标为(1,2),∴-x2+3x=2.即x2-3x+2=0. 解得:x1=2,x2=1(不合题意,舍去)
∴当P点的坐标为(2,3)时,四边形DCEP是平行四边形.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案