题目内容
【题目】数学兴趣小组活动中,小明进行数学探究活动,将边长为![]() 的正方形ABCD与边长为
的正方形ABCD与边长为![]() 的正方形AEFG按图1位置放置,AD与AE在同一条直线上,AB与AG在同一条直线上.
的正方形AEFG按图1位置放置,AD与AE在同一条直线上,AB与AG在同一条直线上.
(1)小明发现DG⊥BE,请你帮他说明理由.
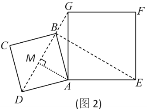
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.


【答案】(1)详见解析;(2)3.
【解析】
(1)根据正方形的性质,得△ADG≌△ABE,所以∠AGD=∠AEB. 延长EB交DG于点H.由图形及题意,得到∠DHE =90°,所以,![]() .(2)根据正方形的性质等,先证明△ADG≌△ABE(SAS) ,得到DG=BE. 过点A作AM⊥DG交DG于点M.由题意,得AM=
.(2)根据正方形的性质等,先证明△ADG≌△ABE(SAS) ,得到DG=BE. 过点A作AM⊥DG交DG于点M.由题意,得AM=![]() BD=1,再由勾股定理,得到GM=2,所以DG=DM+GM=1+2=3,最后得到BE=DG=3.
BD=1,再由勾股定理,得到GM=2,所以DG=DM+GM=1+2=3,最后得到BE=DG=3.
(1)![]() 四边形ABCD与四边形AEFG是正方形
四边形ABCD与四边形AEFG是正方形
∴AD=AB,∠DAG=∠BAE=90°,AG=AE
∴△ADG≌△ABE
∴∠AGD=∠AEB
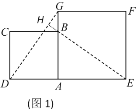
如图1,延长EB交DG于点H
![]() △ADG中 ∠AGD+∠ADG=90°
△ADG中 ∠AGD+∠ADG=90°
∴∠AEB+∠ADG=90°
![]() △DEH中, ∠AEB+∠ADG+∠DHE=180°
△DEH中, ∠AEB+∠ADG+∠DHE=180°
∴∠DHE =90°
∴![]()
(2)![]() 四边形ABCD与四边形AEFG是正方形
四边形ABCD与四边形AEFG是正方形
∴AD=AB, ∠DAB=∠GAE=90°,AG=AE
∴∠DAB+∠BAG=∠GAE+∠BAG
∴∠DAG=∠BAE
![]() AD=AB, ∠DAG=∠BAE,AG=AE
AD=AB, ∠DAG=∠BAE,AG=AE
∴△ADG≌△ABE(SAS)
∴DG=BE
如图2,过点A作AM⊥DG交DG于点M,
∠AMD=∠AMG=90°
![]() BD是正方形ABCD的对角线
BD是正方形ABCD的对角线
∴∠MDA=∠MDA=∠MAB=45°, BD=2
∴AM=![]() BD=1
BD=1
在Rt△AMG中,
∵![]()
∴GM=2
∵DG=DM+GM=1+2=3
∴BE=DG=3

【题目】市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,分别计算甲、乙的平均成绩;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
【题目】在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个,小明做摸球实验,他将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 70 | 128 | 171 | 302 | 481 | 599 | 903 |
摸到白球的频率 | 0.75 | 0.64 | 0.57 | 0.604 | 0.601 | 0.599 | 0.602 |
(1)请估计:当n很大时,摸到白球的概率约为 .(精确到0.1)
(2)估算盒子里有白球 个.
(3)若向盒子里再放入x个除颜色以外其它完全相同的球,这x个球中白球只有1个,每次将球搅拌均匀后,任意摸出一个球记下颜色再放回,通过大量重复摸球试验后发现,摸到白球的频率稳定在50%,那么可以推测出x最有可能是 .