Question

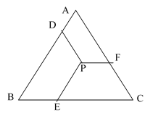
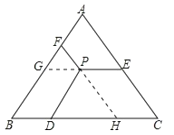
【题目】如图，已知等边△ABC的边长为10，P是△ABC内一点，PD平行AC，PE平行AD，PF平行BC，点D，E，F分别在AB，BC，AC上，则PD+PE+PF= _______________．

Answer 1

【答案】10

【解析】

延长EP、FP分别交AB、BC于G、H，则由PD∥AB，PE∥BC，PF∥AC，可得平行四边形PGBD和平行四边形EPHC，再根据平行四边形及等边三角形的性质得到PD=DH,PE=HC,PF=BD，故可求出PD+PE+PF的长．

如图，延长EP、FP分别交AB、BC于G、H，

由PD∥AB，PE∥BC，PF∥AC，可得平行四边形PGBD和平行四边形EPHC，

∴PG=BD,PE=HC

又∵△ABC是等边三角形，

且PF∥AC，PD∥AB，可得△PFG，△PDH是等边三角形，

∴PF=PG=BD,PD=DH

∴PD+PE+PF=DH+GP+HC=DH+BD+HC=BC=10

故答案为：10．