جâؤ؟ؤعبف
،¾جâؤ؟،؟بçح¼£¬½«ز»¸ِب½ا°ه·إشع±ك³¤خھ1µؤص·½ذخ![]() ةد£¬²¢ت¹ثüµؤض±½ا¶¥µم
ةد£¬²¢ت¹ثüµؤض±½ا¶¥µم![]() شع¶ش½ادك
شع¶ش½ادك![]() ةد»¬¶¯£¬ض±½اµؤز»±كت¼ضص¾¹µم
ةد»¬¶¯£¬ض±½اµؤز»±كت¼ضص¾¹µم![]() £¬ءيز»±كسëةندك
£¬ءيز»±كسëةندك![]() دཻسعµم
دཻسعµم![]() £®
£®

£¨1£©µ±µم![]() شع
شع![]() ±كةدت±£¬¹µم
±كةدت±£¬¹µم![]() ×÷
×÷![]() ·ض±ً½»
·ض±ً½»![]() £¬
£¬![]() سعµم
سعµم![]() £¬
£¬![]() £¬ض¤أ÷£؛
£¬ض¤أ÷£؛![]() £»
£»
£¨2£©µ±µم![]() شعدك¶خ
شعدك¶خ![]() µؤرس³¤دكةدت±£¬ةè
µؤرس³¤دكةدت±£¬ةè![]() ،¢
،¢![]() ء½µم¼نµؤ¾àہëخھ
ء½µم¼نµؤ¾àہëخھ![]() £¬
£¬![]() µؤ³¤خھ
µؤ³¤خھ![]() £®
£®
¢ظض±½سذ´³ِ![]() سë
سë![]() ض®¼نµؤ؛¯ت¹طدµ£¬²¢ذ´³ِ؛¯ت×ش±نء؟
ض®¼نµؤ؛¯ت¹طدµ£¬²¢ذ´³ِ؛¯ت×ش±نء؟![]() µؤب،ضµ·¶خ§£»
µؤب،ضµ·¶خ§£»
¢ع![]() ؤـ·ٌخھµبرüب½اذخ£؟بç¹ûؤـ£¬ض±½سذ´³ِدàس¦µؤ
ؤـ·ٌخھµبرüب½اذخ£؟بç¹ûؤـ£¬ض±½سذ´³ِدàس¦µؤ![]() ضµ£»بç¹û²»ؤـ£¬ثµأ÷ہيسة£®
ضµ£»بç¹û²»ؤـ£¬ثµأ÷ہيسة£®
،¾´ً°¸،؟£¨1£©¼û½âخِ£»£¨2£©¢ظ £®¢ع
£®¢ع![]() ؤـخھµبرüب½اذخ£¬
ؤـخھµبرüب½اذخ£¬![]() £®
£®
،¾½âخِ،؟
£¨1£©¸ù¾فص·½ذخµؤذشضتض¤أ÷![]() £¬¼´؟ةاَ½â£»
£¬¼´؟ةاَ½â£»
£¨2£©¢ظ¸ù¾فجâزâ×÷ح¼£¬سةص·½ذخµؤذشضت؟ةضھµ±![]() ت±£¬µم
ت±£¬µم![]() شعدك¶خ
شعدك¶خ![]() µؤرس³¤دكةد£¬ح¬ہي؟ةµأ
µؤرس³¤دكةد£¬ح¬ہي؟ةµأ![]() £¬µأµ½MP=NQ£¬ہûسأµبرüض±½اب½اذخµؤذشضت؟ةضھMP=
£¬µأµ½MP=NQ£¬ہûسأµبرüض±½اب½اذخµؤذشضت؟ةضھMP=![]() x£¬NC=CD-DN=1-
x£¬NC=CD-DN=1-![]() x£¬CQ=y£¬´ْبëMP=NQ»¯¼ٍ¼´؟ةاَ½â£»
x£¬CQ=y£¬´ْبëMP=NQ»¯¼ٍ¼´؟ةاَ½â£»
¢عسة![]() تاµبرüب½اذخ£¬،دPCQ=135،م£¬CP=CQ³ةء¢£¬´ْبë½â·½³ج¼´؟ةاَ½â £¬
تاµبرüب½اذخ£¬،دPCQ=135،م£¬CP=CQ³ةء¢£¬´ْبë½â·½³ج¼´؟ةاَ½â £¬
£¨1£©ض¤أ÷£؛،كشعص·½ذخ![]() ضذ£¬
ضذ£¬![]() خھ¶ش½ادك£¬
خھ¶ش½ادك£¬
،à![]() £¬
£¬![]() £¬،ك
£¬،ك![]() £¬
£¬
،à![]() £¬
£¬![]() £¬
£¬
،à![]() £¬
£¬
سض،ك![]() £¬
£¬
،à![]() £®
£®
،ك![]() £¬،à
£¬،à![]() £®
£®
سض،ك![]() £¬،à
£¬،à![]() £¬
£¬
،à![]() £¬
£¬
شع![]() ضذ£¬
ضذ£¬
،ك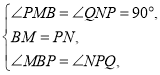
،à![]() £¬،à
£¬،à![]() £®
£®
£¨2£©¢ظبçح¼£¬µم![]() شعدك¶خ
شعدك¶خ![]() µؤرس³¤دكةد£¬
µؤرس³¤دكةد£¬
ح¬£¨1£©؟ةض¤![]() £¬
£¬
،àMP=NQ£¬
شعµبرüض±½اب½اذخAMPضذ£¬AP=![]() =x
=x
،àMP=![]() x=AM,
x=AM,
،àNC=BM=AB-AM=1-![]() x
x
¹تNQ=NC+CQ=1-![]() x+y
x+y
،à![]() x=1-
x=1-![]() x+y
x+y
»¯¼ٍµأ![]()
µ±Pµمخ»سعACضذµمت±£¬Qµما،؛أشعCµم£¬سضAP£¼AC=![]()
،à![]()
،à![]() سë
سë![]() ض®¼نµؤ؛¯ت¹طدµتا
ض®¼نµؤ؛¯ت¹طدµتا![]() £¨
£¨![]() £©
£©
¢عµ±![]() ت±£¬
ت±£¬![]() ؤـخھµبرüب½اذخ£¬
ؤـخھµبرüب½اذخ£¬
ہيسة£؛µ±µم![]() شع
شع![]() µؤرس³¤دكةد£¬CQ=
µؤرس³¤دكةد£¬CQ=![]() £¬CQ=AC-AP=
£¬CQ=AC-AP=![]() £¬
£¬
سة![]() تاµبرüب½اذخ£¬،دPCQ=،دPCB+،دBCQ=45،م+90،م=135،م£¬
تاµبرüب½اذخ£¬،دPCQ=،دPCB+،دBCQ=45،م+90،م=135،م£¬
،àCP=CQ³ةء¢£¬
¼´![]() ت±£¬½âµأ
ت±£¬½âµأ![]() £®
£®

 جىجىدٍةدز»±¾؛أ¾يدµءذ´ً°¸
جىجىدٍةدز»±¾؛أ¾يدµءذ´ً°¸ ذ،ر§ةْ10·ضضسس¦سأجâدµءذ´ً°¸
ذ،ر§ةْ10·ضضسس¦سأجâدµءذ´ً°¸،¾جâؤ؟،؟خھءثدىس¦تذخ¯؛حتذص¸®،°آجة«»·±££¬½عؤـ¼ُإإ،±µؤ؛إصظ£¬ذز¸£ةج³،سأ3300شھ¹؛½ّ¼×،¢ززء½ضض½عؤـµئ¹²¼ئ100ض»£¬؛ـ؟ىتغح꣮صâء½ضض½عؤـµئµؤ½ّ¼غ،¢تغ¼غبçدآ±ي£؛
½ّ¼غ£¨شھ/ض»£© | تغ¼غ£¨شھ/ض»£© | |
¼×ضض½عؤـµئ | 30 | 40 |
¼×ضض½عؤـµئ | 35 | 50 |
£¨1£©اَذز¸£ةج³،¼×،¢ززء½ضض½عؤـµئ¸÷¹؛½ّءث¶àةظض»£؟
£¨2£©ب«²؟تغحê100ض»½عؤـµئ؛َ£¬ةج³،¹²¼ئ»ٌہû¶àةظشھ£؟
،¾جâؤ؟،؟µ±ذذت»ضذµؤئû³µ×²µ½خïجهت±£¬ئû³µµؤثً»µ³ج¶بح¨³£سأ،°×²»÷س°دى،±ہ´؛âء؟£®ئû³µµؤײ»÷س°دىI؟ةزشسأئû³µذذت»ثظ¶بv(km/min)ہ´±يت¾£¬دآ±يتاؤ³ضضذح؛إئû³µµؤذذت»ثظ¶بسëײ»÷س°دىµؤتشرéت¾ف£؛
v(km/min) | 0 | 1 | 2 | 3 | 4 |
I | 0 | 2 | 8 | 18 | 32 |
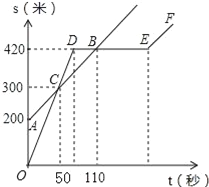
(1)اë¸ù¾فةد±يضذµؤت¾ف£¬شعض±½ا×ّ±êدµضذأè³ِ×ّ±ê(v£¬I)ثù¶شس¦µؤµم£¬²¢سأ¹â»¬اْدك½«¸÷µمء¬½سئًہ´£»

(2)جîذ´دآ±ي£¬²¢¸ù¾ف±يضذت¾فµؤ³تدض¹وآة£¬²آدëسأv±يت¾Iµؤ¶´خ؛¯ت±ي´ïت½£»
v(km/min) | 1 | 2 | 3 | 4 |
|
|
|
|
|
(3)µ±ئû³µµؤثظ¶ب·ض±ًتا1.5 km/min£¬2.5 km/min£¬4.5 km/minت±£¬ہûسأؤمµأµ½µؤײ»÷س°دى¹«ت½£¬¼ئثمײ»÷س°دى·ض±ًتا¶àةظ£؟