题目内容
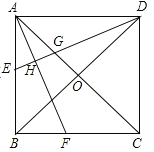
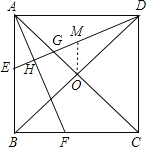
【题目】如图，正方形ABCD中，O是对角线的交点，AF平分
BAC，DH
AF于点H，交AC于G，DH延长线交AB于点E，求证：BE=2OG.
【答案】证明见解析.
【解析】作OM∥AB交DE于M．首先证明OM是△DEB的中位线，再根据等角对等边证明OG=OM即可解决问题．
作OM∥AB交DE于M．
∵四边形ABCD是正方形，
∴OB=OD，
∵OM∥BE，
∴EM=DM，
∴BE=2OM，
∵∠OAD=∠ADO=∠BAC=45°，
∵AF平分∠BAC，
∴∠EAH=22.5°，
∵AF⊥DE，
∴∠AHE=∠AHD=90°，
∴∠AEH=67.5°，
∵∠ADE+∠AED=90°，
∴∠ADE=22.5°，
∴∠OGD=∠GAD+∠ADE=67.5°，
∵∠AEH=∠OME=67.5°，
∴∠OGM=∠OMG，
∴OG=OM，
∴BE=2OG．
【题目】为减少环境污染，自2008年6月1日起，全国的商品零售场所开始实行“塑料购物袋有偿使用制度”（以下简称“限塑令”）．某班同学于6月上旬的一天，在某超市门口采用问卷调查的方式，随机调查了“限塑令”实施前后，顾客在该超市用购物袋的情况，以下是根据100位顾客的100份有效答卷画出的统计图表的一部分：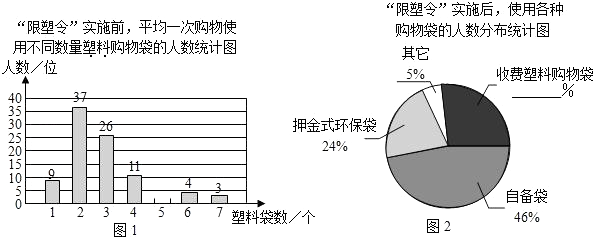 
“限塑令”实施后，塑料购物袋使用后的处理方式统计表：
处理方式 | 直接丢弃 | 直接做垃圾袋 | 再次购物使用 | 其它 |
选该项的人数占 | 5% | 35% | 49% | 11% |
请你根据以上信息解答下列问题：
（1）补全图1，“限塑令”实施前，如果每天约有2 000人次到该超市购物．根据这100位顾客平均一次购物使用塑料购物袋的平均数，估计这个超市每天需要为顾客提供多少个塑料购物袋？
（2）补全图2，并根据统计图和统计表说明，购物时怎样选用购物袋，塑料购物袋使用后怎样处理，能对环境保护带来积极的影响．