Question

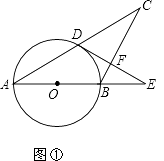
【题目】《九章算术》“勾股”章的问题：：“今有二人同所立，甲行率七，乙行率三，乙东行，甲南行十步而斜东北与乙会.问甲、乙各行几何？”大意是说：如图，甲乙二人从A处同时出发，甲的速度与乙的速度之比为7:3，乙一直向东走，甲先向南走十步到达C处，后沿北偏东某方向走了一段距离后与乙在B处相遇，这时，甲乙各走了多远？

Answer 1

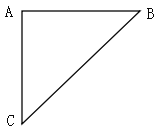
【答案】甲行24.5步，乙行10.5步．

【解析】甲乙同时出发二者速度比是7:3，设相遇时甲行走了7t，乙行走了3t根据二者的路程关系可列方程求解.

设经x秒二人在B处相遇，这时乙共行AB=3x，

甲共行AC+BC=7x，

∵AC=10，

∴BC=7x-10，

又∵∠A=90°，

∴BC2=AC2+AB2，

∴（7x-10）2=102+（3x）2，

解得：x1=0（舍去），x2=3.5，

∴AB=3x=10.5，

AC+BC=7x=24.5．

答：甲行24.5步，乙行10.5步．