Question

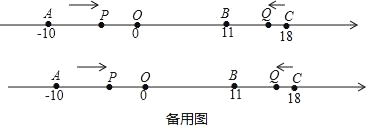
【题目】如图，在数轴上，点A表示﹣10，点B表示11，点C表示18．动点P从点A出发，沿数轴正方向以每秒2个单位的速度匀速运动；同时，动点Q从点C出发，沿数轴负方向以每秒1个单位的速度匀速运动．设运动时间为t秒．

（1）当t为何值时，P、Q两点相遇？相遇点M所对应的数是多少？

（2）在点Q出发后到达点B之前，求t为何值时，点P到点O的距离与点Q到点B的距离相等；

（3）在点P向右运动的过程中，N是AP的中点，在点P到达点C之前，求2CN﹣PC的值．

Answer 1

【答案】（1）t=， M所对应的数是；（2）t的值为3或；（3）28．

【解析】

(1) 根据题意, 由P、 Q两点的路程和为28路程方程求解即可;

(2) 由题意得,t的值大于0且小于7. 分点P在点O的左边, 点P在点O的右边两种情况讨论即可求解;

(3) 根据中点的定义得到AN=PN=AP=t,可得CN=AC-AN=28-t, PC=28-AP=28-2t, 再代入计算即可求解.

解：（1）根据题意得2t+t=28，

解得t=，

∴AM=＞10，

∴M在O的右侧，且OM=﹣10=，

∴当t=时，P、Q两点相遇，相遇点M所对应的数是；

（2）由题意得，t的值大于0且小于7．

若点P在点O的左边，则10﹣2t=7﹣t，解得t=3．

若点P在点O的右边，则2t﹣10=7﹣t，解得t=．

综上所述，t的值为3或时，点P到点O的距离与点Q到点B的距离相等；

（3）∵N是AP的中点，

∴AN=PN=AP=t，

∴CN=AC﹣AN=28﹣t，PC=28﹣AP=28﹣2t，

2CN﹣PC=2（28﹣t）﹣（28﹣2t）=28．