题目内容
【题目】在△ABC中,P为边AB上一点.
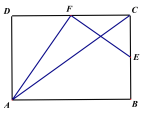
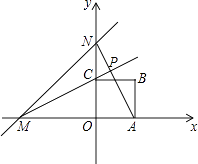
(1)如图1,若∠ACP=∠B,求证:AC2=APAB;
(2)若M为CP的中点,AC=2.
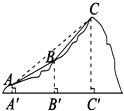
①如图2,若∠PBM=∠ACP,AB=3,求BP的长;
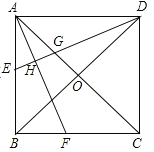
②如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.
【答案】
(1)
解:∵∠ACP=∠B,∠A=∠A,
∴△ACP∽△ABC,
∴ ![]() ,
,
∴AC2=APAB
(2)
解:①取AP在中点G,连接MG,
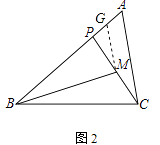
设AG=x,则PG=x,BG=3﹣x,
∵M是PC的中点,
∴MG∥AC,
∴∠BGM=∠A,
∵∠ACP=∠PBM,
∴△APC∽△GMB,
∴ ![]() ,
,
即 ![]() ,
,
∴x= ![]() ,
,
∵AB=3,
∴AP=3﹣ ![]() ,
,
∴PB= ![]() ;
;
②过C作CH⊥AB于H,延长AB到E,使BE=BP,
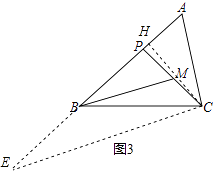
设BP=x.
∵∠ABC=45°,∠A=60°,
∴CH= ![]() ,HE=
,HE= ![]() +x,
+x,
∵CE2= ![]() +(
+( ![]() +x)2,
+x)2,
∵PB=BE,PM=CM,
∴BM∥CE,
∴∠PMB=∠PCE=60°=∠A,
∵∠E=∠E,
∴△ECP∽△EAC,
∴ ![]() ,
,
∴CE2=EPEA,
∴3+3+x2+2 ![]() x=2x(x+
x=2x(x+ ![]() +1),
+1),
∴x= ![]() ﹣1,
﹣1,
∴PB= ![]() ﹣1.
﹣1.
【解析】(1)根据相似三角形的判定定理即可得到结论;(2)①取AP在中点G,连接MG,设AG=x,则PG=x,BG=3﹣x,根据三角形的中位线的性质得到MG∥AC,由平行线的性质得到∠BGM=∠A,∵∠根据相似三角形的性质得到 ![]() ,求得x=
,求得x= ![]() ,即可得到结论;②过C作CH⊥AB于H,延长AB到E,使BE=BP解直角三角形得到CH=
,即可得到结论;②过C作CH⊥AB于H,延长AB到E,使BE=BP解直角三角形得到CH= ![]() ,HE=
,HE= ![]() +x,根据勾股定理得到CE2=
+x,根据勾股定理得到CE2= ![]() +9
+9 ![]() +x)2根据相似三角形的性质得到CE2=EPEA列方程即可得到结论.
+x)2根据相似三角形的性质得到CE2=EPEA列方程即可得到结论.

 阅读快车系列答案
阅读快车系列答案【题目】射击队为从甲、乙两名运动员选拔一人参加运动会,对他们进行了六次测试,测试成绩如下表(单位:环)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)由表格中的数据,计算出甲的平均成绩是 环,乙的成绩是 环.
(2)结合平均水平与发挥稳定性你认为推荐谁参加比赛更适合,请说明理由.