题目内容
【题目】快车与慢车分別从甲乙两地同时相向出发,匀速而行,快车到达乙地后停留 1h,然后按原路原速返回, 快车比慢车晚 1h 到达甲地,快慢两车距各自出发地的路程 y(km)与所用的时间 x(h)的关系如图所示.
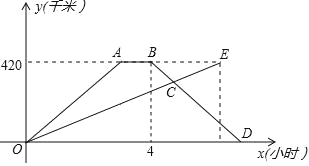
(1)甲乙两地之间的路程为 km;快车的速度为 km/h;慢车的速度为 km/h ;
(2)出发 h,快慢两车距各自出发地的路程相等;(写出解答过程快慢两车出发 h 相距 150km.(写出解答过程)
【答案】(1)420;140;70(2)![]() ;
;![]() 或
或![]() 或
或![]()
【解析】
(1)先得两地的距离,根据速度=路程÷时间列式计算即可求出快车和慢车的速度;
(2)由图可知:快车返程时,两车距各自出发地的路程相等,根据慢车的路程=2个总路程快车的路程,列方程即可得出答案;分别根据两车相遇以及两车相遇后两车距离为150km时,列方程可解答.
(1)由图可知:甲乙两地之间的路程为420km;
快车的速度为:![]() =140km/h;
=140km/h;
由题意得:快车7小时到达甲地,则慢车6小时到达甲地,
则慢车的速度为:![]() =70km/h;
=70km/h;
故答案为:420,140,70;
(2)∵快车速度为:140km/h,
∴A点坐标为;(3,420),
∴B点坐标为(4,420),
由图可知:快车返程时,两车距各自出发地的路程相等,
设出发x小时,两车距各自出发地的路程相等,
70x=2×420140(x1),
70x=98014x,
解得:x=![]() ,
,
答:出发![]() 小时,快、慢两车距各自出发地的路程相等;
小时,快、慢两车距各自出发地的路程相等;
故答案为:![]() ;
;
第一种情形第一次没有相遇前,相距150km,
则140x+70x+150=420,
解得:x=![]() ,
,
第二种情形应是相遇后而快车没到乙地前140x+70x420=150,
解得:x=![]() ,
,
第三种情形是快车从乙往甲返回:70x140(x4)=150,
解得:x=![]() ,
,
综上所述:快慢两车出发![]() h或
h或![]() h或
h或![]() h相距150km.
h相距150km.
故答案为:![]() 或
或![]() 或
或![]() .
.