Question

【题目】（1）如图1，△ABC中，D是BC边上一点，则△ABD与△ADC有一个相同的高，它们的面积之比等于相应的底之比，记为（△ABD、△ADC的面积分别用记号、表示）．现有，则 ．

（2）如图2，△ABC中，E、F分别是BC、AC边上一点，且有， ，AE与BF相交于点G．现作EH∥BF交AC于点H．依次求、、的值．

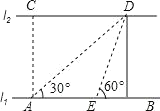
（3）如图3，△ABC中，点P在边AB上，点M、N在边AC上，且有， ，

BM、BN与CP分别相交于点R、Q．现已知△ABC的面积为1，求△BRQ的面积．

Answer 1

【答案】（1）1：3；

（2）， ， ；

（3）．

【解析】试题分析：(1)、根据三角形的面积之比等于底边的比得出答案；(2)、根据相似三角形的性质得出边的比值；(3)、根据题意得出BR:RM=3：2，BQ:QN=3：1，CQ:QR:RP=5：3：2，从而得出和，从而得出答案.

试题解析：（1）1：3

（2）、、

（3）、、

△ABC的面积为1．则 ．