Question

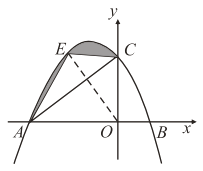
【题目】如图，已知抛物线与轴交于点(点在点的左侧)，与轴交于．

求点的坐标；

若点是抛物线在第二象限部分上的一动点，其横坐标为求为何值时，图中阴影部分面积最小，并写出此时点的坐标．

Answer 1

【答案】（1）点的坐标为；点的坐标为；点坐标为； （2）当时，有最大值，此时阴影部分面积最小，点的坐标为．

【解析】

(1)当y=0时求出得到点A、B的坐标，当x=0时y=4，得到点C的坐标；

(2) 连接根据，利用抛物线的性质得到当时，有最大值，此时阴影部分面积最小，由此得到点的坐标.

当时，

解得

点的坐标为点的坐标为；

当时，，

点坐标为；

点横坐标为又在抛物线上，

点的纵坐标为，

连接

，

抛物线开口向下，当时，有最大值，

此时阴影部分面积最小，

∴点的坐标为.