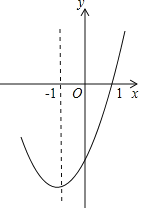题目内容
【题目】如图,一条抛物线与x轴相交于M,N两点(点M在点N的左侧),其顶点P在线段AB上移动,点A,B的坐标分别为(-2,-3),(1,-3),点N的横坐标的最大值为4,则点M的横坐标的最小值为( )

A.-1 B.-3C.-5D.-7
【答案】C
【解析】
当抛物线的顶点在线段AB的B点上时,点N的横坐标最大,把B的坐标代入即可求出a的值,因为抛物线的a是定值.根据题意可知当抛物线的顶点运动到A时,M的横坐标最小,把A的坐标和a的值代入即可求出二次函数的解析式,再求出y=0时x的值即可求出答案.
解:当图象顶点在点B时,点N的横坐标的最大值为4,
则此时抛物线的表达式为:y=a(x1)23,
把点N的坐标代入得:0=a(41)23,
解得:a=![]() ,
,
当顶点在点A时,M点的横坐标为最小,
此时抛物线的表达式为:y=![]() (x+2)2-3,
(x+2)2-3,
令y=0,则x=5或1,
即点M的横坐标的最小值为5,
故答案为:C.

练习册系列答案
相关题目