题目内容
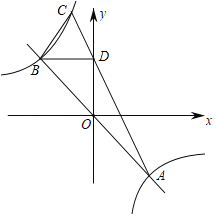
【题目】如图,抛物线y=ax2+bx+4与x轴交于点A(﹣2,0)和B(4,0)、与y轴交于点C.点M,Q分别从点A,B以每秒1个单位长度的速度沿x轴同时出发相向而行.当点M到达原点时,点Q立刻掉头并以每秒![]() 个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动.过点M的直线l⊥x轴,交AC或BC于点P.当t=_____时,△APQ的面积S有最大值,为_____.
个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动.过点M的直线l⊥x轴,交AC或BC于点P.当t=_____时,△APQ的面积S有最大值,为_____.
【答案】![]() ;
; ![]() .
.
【解析】
把A,B的坐标代入y=ax2+bx+4求得抛物线的解析式,①当0<t≤2时,△AMP∽△AOC,得出![]() ,用含t的式子表示出PM,AQ,然后求出面积S的表达式,利用配方法求出最值;②当2<t≤3时,作PM⊥x轴于M,PF⊥y轴于点F,同①用含t的式子表示出PM,AQ,然后求出面积S的表达式,利用配方法求出最值即可.
,用含t的式子表示出PM,AQ,然后求出面积S的表达式,利用配方法求出最值;②当2<t≤3时,作PM⊥x轴于M,PF⊥y轴于点F,同①用含t的式子表示出PM,AQ,然后求出面积S的表达式,利用配方法求出最值即可.
解:把A(﹣2,0),B(4,0)代入y=ax2+bx+4得:
![]() ,解得:
,解得: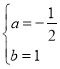 ,
,
∴抛物线的解析式是:y=﹣![]() x2+x+4,
x2+x+4,
∴C(0,4),对称轴为x=1,
∴AO=2,CO=BO=4,AB=AO+BO=6,
①当0<t≤2时,
∵MP∥CO,∴△AMP∽△AOC,
∴![]() ,∴PM=
,∴PM=![]() =2t,
=2t,
又AQ=6﹣t,
∴S=![]() PMAQ=
PMAQ=![]() ×2t(6﹣t)=﹣t2+6t=﹣(t﹣3)2+9,
×2t(6﹣t)=﹣t2+6t=﹣(t﹣3)2+9,
当t=2时,S取最大值,最大值为8;
②当2<t≤3时,作PM⊥x轴于M,作PF⊥y轴于点F,
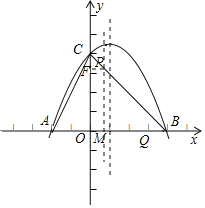
则FP∥BO,∴△COB∽△CFP,
∵CO=OB,∴FP=FC=t﹣2,∴PM=OF=4﹣(t﹣2)=6﹣t,
又AQ=4+![]() (t﹣2)=
(t﹣2)=![]() t+1,
t+1,
∴S=![]() PMAQ=
PMAQ=![]() (6﹣t)(
(6﹣t)(![]() t+1)=﹣
t+1)=﹣![]() t2+4t+3=﹣
t2+4t+3=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
当t=![]() 时,S取最大值,最大值为
时,S取最大值,最大值为![]() ,
,
综上所述,当t=![]() 时,S取最大值,最大值为
时,S取最大值,最大值为![]() .
.
故答案为:![]() ;
;![]() .
.

练习册系列答案
相关题目