Question

【题目】如图，是等边三角形，，点是射线上任意点（点与点不重合），连接，将线段绕点顺时针旋转得到线段，连接并延长交直线于点．

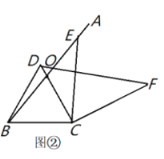
（1）如图①，猜想的度数是__________；

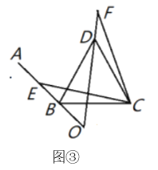
（2）如图②，图③，当是锐角或钝角时，其他条件不变，猜想的度数，并选取其中一种情况进行证明；

（3）如图③，若，，，则的长为__________．

Answer 1

【答案】（1）；（2），证明见解析；（3） ．

【解析】

（1）根据等边三角形的性质可得，，然后根据旋转的性质可得，°，从而得出，然后利用SAS即可证出，最后利用对顶角相等和三角形的内角和定理即可求出结论；

（2）根据等边三角形的性质可得，，然后根据旋转的性质可得，°，从而得出，然后利用SAS即可证出，最后利用对顶角相等和三角形的内角和定理即可求出结论；

（3）设EC和FO交于点G，根据等边三角形的性质可得，，然后根据旋转的性质可得，°，从而得出、∠DCG=45°、∠BEC=30°，然后利用SAS即可证出，从而可求∠FGC=90°，然后根据等腰直角三角形的性质、勾股定理和30°所对的直角边是斜边的一半即可得出结论．

解：（1） ∵是等边三角形，

∴，．

∵线段绕点顺时针旋转60°得到线段,

∴，°．

∴，

即．

在和中

∴．

∴．

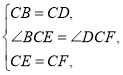
又，，．

∴．

（2）．

证明：如图②，是等边三角形，

∴，．

∵线段绕点顺时针旋转60°得到线段,

∴，°．

∴，

即．

在和中

∴．

∴．

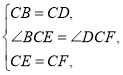
又，，．

∴．

（3）设EC和FO交于点G

∵是等边三角形，

∴，．

∵线段绕点顺时针旋转60°得到线段,

∴，°．

∴，

即．

∴∠DCG=∠ECF－∠DCF=45°

∵

∴∠BEC=180°－∠ABC－∠BCE=30°

在和中

∴．

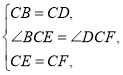
∴=30°

∴∠FGC=180°－∠F－∠ECF=90°

∴△CGD为等腰直角三角形，CG= DG

∴CG 2+DG2=CD2

即2CG2=62

解得：CG= DG=

在Rt△FGC中，FC=2CG =，FG=

∴DF=FG－DG=－