Question

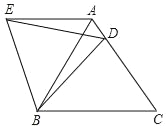
【题目】如图，△ABC中，AB＝AC，D是BC中点，F是AC中点，AN是△ABC的外角∠MAC的角平分线，延长DF交AN于点E，连接CE．

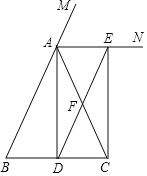
（1）求证：四边形ADCE是矩形；

（2）填空：①若BC＝AB＝4，则四边形ABDE的面积为　　．

②当△ABC满足　　时，四边形ADCE是正方形．

Answer 1

【答案】（1）见解析；（2）①4，②∠BAC＝90°

【解析】

（1）利用角平分线、等边对等角和外角可先证出∠MAE＝∠B，所以AN∥BC，利用F是AC的中点可证△AFE≌△CFD，即可得到EF=FD，利用对角线互相平分的四边形是平行四边形所以四边形ADCE为平行四边形，再利用AB＝AC，点D为BC中点，可以得到AD⊥BC，

有一个角是直角的平行四边形是矩形可得：四边形ADCE为矩形；

（2）由D、F分别是BC、AC的中点，利用中位线的性质可得：DF∥AB，易证四边形ABDE是平行四边形，利用BC＝AB＝4，AB＝AC，可得△ABC是等边三角形，最后利用锐角三角函数求出高AD即可.

（3）可根据四边形ADCE是矩形，若再有一组邻边相等即为正方形不防使AD=DC，此时不难发现△ADC为等腰直角三角形，故∠ACB=45°，再根据△ABC为等腰三角形，即可得到∠BAC=90°.

证明：∵AN是△ABC外角∠CAM的平分线，

∴∠MAE＝∠MAC，

∵∠MAC＝∠B+∠ACB，

∵AB＝AC，

∴∠B＝∠ACB，

∴∠MAE＝∠B，

∴AN∥BC，

∴∠EAF=∠DCF

在△AFE和△CFD中

∴△AFE≌△CFD

∴EF=FD

∴四边形ADCE为平行四边形

∵AB＝AC，点D为BC中点，

∴AD⊥BC，

∴∠ADC＝90°，

∴四边形ADCE为矩形；

（2）①解：∵AB＝AC，D是BC中点，F是AC中点，

∴DF∥AB，

由（1）知AE∥BD，

∴四边形ABDE是平行四边形，

∵BC＝AB＝4，AB＝AC，

∴△ABC是等边三角形，

∴∠ABD＝60°，

∵D为BC的中点，

∴∠ADC＝90°，BD＝2，

∴，

∴四边形ABDE的面积为BD×AD＝2×＝4，

故答案为：4；

②解：答案不唯一，如当∠BAC＝90°时，四边形ADCE是正方形．

∵∠BAC＝90°，AB＝AC，

∴△ABC为等腰直角三角形，

∵D为BC的中点，

∴AD＝DC，

∵四边形ADCE为矩形，

∴四边形ADCE为正方形．

故答案为：∠BAC＝90°．