题目内容
【题目】如图,某数学兴趣小组开展以下折纸活动:①对折矩形纸片ABCD,使AD和BC重合,得到折痕EF,把纸片展开;②再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN.观察探究可以得到∠NBC的度数是( )

A. 20°B. 25°C. 30°D. 35°
【答案】C
【解析】
BM交EF于P,如图,根据折叠的性质得∠BNM=∠A=90°,∠2=∠3,EF∥AD,AE=BE,则可判断EP为△BAM的中位线,利用平行线的性质得∠1=∠NBC,根据斜边上的中线性质得PN=PB=PM,所以∠1=∠2,从而得到∠NBC=∠2=∠3,然后利用∠NBC+∠2+∠3=90°可得到∠NBC的度数.
BM交EF于P,如图,
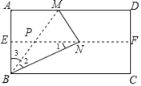
∵四边形ABCD为矩形,
∴∠A=∠ABC=90°,
∵折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,
∴∠BNM=∠A=90°,∠2=∠3,
∵对折矩形纸片ABCD,使AD和BC重合,得到折痕EF,
∴EF∥AD,AE=BE,
∴EP为△BAM的中位线,∠1=∠NBC,
∴P点为BM的中点,
∴PN=PB=PM,
∴∠1=∠2,
∴∠NBC=∠2=∠3,
∵∠NBC+∠2+∠3=90°,
∴∠NBC=30°.
故选C.

【题目】某水果公司购进10 000kg苹果,公司想知道苹果的损坏率,从所有苹果中随机抽取若干进行统计,部分结果如下表:
苹果总质量n(kg) | 100 | 200 | 300 | 400 | 500 | 1000 |
损坏苹果质量m(kg) | 10.50 | 19.42 | 30.63 | 39.24 | 49.54 | 101.10 |
苹果损坏的频率 (结果保留小数点后三位) | 0.105 | 0.097 | 0.102 | 0.098 | 0.099 | 0.101 |
估计这批苹果损坏的概率为_____(结果保留小数点后一位),损坏的苹果约有______kg.
【题目】南果梨是东北辽宁省的一大特产,现有20筐南国梨,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值 (单位:千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐南果梨中,最重的一筐比最轻的一筐重多少千克?
(2)与标准重量比较,20筐南果梨总计超过或不足多少千克?
(3)若南果梨每千克售价4元,则这20筐可卖多少元?