题目内容
如图,平面直角坐标系中,⊙O1过原点O,且⊙O1与⊙O2相外切,圆心O1与O2在x轴正半轴上,⊙O1的半径O1P1、⊙O2的半径O2P2都与x轴垂直,且点P1 、P2
、P2 在反比例函数
在反比例函数 (x>0)的图象上,则
(x>0)的图象上,则 .
.

【答案】
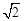 。
。
【解析】∵⊙O1过原点O,⊙O1的半径O1P1,∴O1O=O1P1。
∵⊙O1的半径O1P1与x轴垂直,点P1(x1,y1)在反比例函数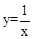 (x>0)的图象上,
(x>0)的图象上,
∴x1=y1,x1y1=1。∴x1=y1=1。
∵⊙O1与⊙O2相外切,⊙O2的半径O2P2与x轴垂直,
设两圆相切于点A,
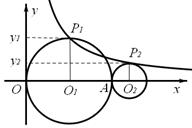
∴AO2=O2P2=y2,OO2=2+y2。
∴P2点的坐标为:(2+y2,y2)。
∵点P2在反比例函数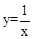 (x>0)的图象上,
(x>0)的图象上,
∴(2+y2)•y2=1,解得:y2=-1+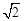 或-1-
或-1-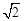 (不合题意舍去)。
(不合题意舍去)。
∴y1+y2=1+(-1+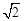 )=
)= 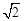 。
。

练习册系列答案
相关题目
 如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线
如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线 =2
=2 如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.