题目内容
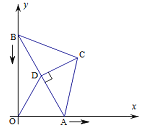
【题目】如图，正方形ABCD的边长为2，H在CD的延长线上，四边形CEFH也为正方形，则△DBF的面积为 ．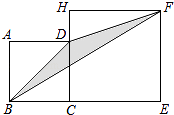 
【答案】2
【解析】解：设正方形CEFH的边长为a，根据题意得：
S△BDF=S正方形ABCD+S正方形CEFH﹣S△ABD﹣S△DHF﹣S△BEF
=4+a2﹣ 
×4﹣ a（a﹣2）﹣ a（a+2）
=2+a2﹣ a2+a﹣ a2﹣a
=2．
所以答案是：2．
方法二：连接CF．易证BD∥CF， 
∴S△BDF=S△BDC= S正方形ABCD=2．
【考点精析】根据题目的已知条件，利用三角形的面积和正方形的性质的相关知识可以得到问题的答案，需要掌握三角形的面积=1/2×底×高；正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
