题目内容

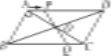
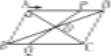
【题目】如图，在平行四边形ABCD中，E、F分别是边BC、AD上的点，有下列条件：

①AE∥CF；②BE＝FD；③∠1＝∠2；④AE＝CF.

若要添加其中一个条件，使四边形AECF一定是平行四边形，则添加的条件可以是(　 　)

A. ①②③④ B. ①②③ C. ②③④ D. ①③④

【答案】B

【解析】

由四边形ABCD是平行四边形，可得AD∥BC，AD=BC，∠BAD=∠BCD，然后利用平行四边形的判定分别分析求解，即可求得答案；注意利用举反例的方法可排除错误答案．

∵四边形ABCD是平行四边形，

∴AD∥BC，AD=BC，∠BAD=∠BCD，

∴当①AE∥CF时，四边形AECF是平行四边形；故①正确；

当②BE=FD时，CE=AF，则四边形AECF是平行四边形；故②正确；

当③∠1=∠2时，∠EAF=∠ECF，

∵∠EAF+∠AEC=180,∠AFC+∠ECF=180，

∴∠AFC=∠AEC，

∴四边形AECF是平行四边形；故③正确；

④若AE=AF，则四边形AECF是平行四边形或等腰梯形，故④错误.

故选B.

练习册系列答案
相关题目

【题目】如图，矩形ABCD中，P为AD边上一点，沿直线BP将△ABP翻折至△EBP（点A的对应点为点E），PE与CD相交于点O，且OE=OD．

（1）求证：PE=DH；

（2）若AB=10，BC=8，求DP的长．

【答案】（1）见解析；（2）．

【解析】试题分析：(1) 先证明△DOP≌△EOH，再利用等量代换得到PE=DH.

(2) 设DP=x， Rt△BCH中，先用 x表示三角形三边，利用勾股定理列式解方程.

试题解析：

（1）解：证明：∵OD=OE，∠D=∠E=90°，∠DOP=∠EOH，

∴△DOP≌△EOH，

∴OP=OH，

∴PO+OE=OH+OD，

∴PE=DH.

（2）解：设DP=x，则EH=x，BH=10﹣x，

CH=CD﹣DH=CD﹣PE=10﹣（8﹣x）=2+x，

∴在Rt△BCH中，BC2+CH2=BH2

（2+x）2+82=（10﹣x）2，

∴x=,

∴DP=．

【题型】解答题
【结束】
25

【题目】某文教店老板到批发市场选购A，B两种品牌的绘图工具套装，每套A品牌套装进价比B品牌每套套装进价多2.5元，已知用200元购进A种套装的数量是用75元购进B种套装数量的2倍．

（1）求A，B两种品牌套装每套进价分别为多少元？

（2）若A品牌套装每套售价为13元，B品牌套装每套售价为9.5元，店老板决定，购进B品牌的数量比购进A品牌的数量的2倍还多4套，两种工具套装全部售出后，要使总的获利超过120元，则最少购进A品牌工具套装多少套？

【题目】与在平面直角坐标系中的位置如图所示．

（1）分别写出各点的坐标：___________，_________，_______________．

（2）是由经过怎样的平移变换得到的？答：___________________．

（3）若点是内部一点，则内部的对应点的坐标为___________．

（4）求的面积．

【题目】“低碳环保，绿色出行”的概念得到广大群众的接受，越来越多的人喜欢选择骑自行车作为出行工具．小军和爸爸同时骑车去图书馆，爸爸先以150米/分的速度骑行一段时间，休息了5分钟，再以m米/分的速度到达图书馆．小军始终以同一速度骑行，两人骑行的路程为y(米)与时间x(分钟)的关系如图．请结合图象，解答下列问题：

(1)填空：a=________；b=________；m=________．

(2)若小军的速度是 120 米/分，求小军第二次与爸爸相遇时距图书馆的距离．

(3)在(2)的条件下，爸爸自第二次出发后，骑行一段时间后与小军相距100 米，此时 小军骑行的时间为________分钟．

【题目】(1)如图①，已知直线l1∥l2，且l3和l1，l2分别交于A，B两点，点P在线段AB上，则∠1，∠2，∠3之间的等量关系是____；

(2)如图②，点A在B处北偏东40°方向，在C处北偏西45°方向，则∠BAC＝____°.

(3)如图③，∠ABD和∠BDC的平分线交于点E，BE交AB于点F，∠1＋∠2＝90°，试说明：AB∥AB，并探究∠2与∠3的数量关系．

【题目】如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过第2017次运动后，动点P的坐标是______．

【题目】如图①，OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=5，OC=4．

（1）在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，则D点的坐标；E点的坐标 ．
（2）如图②，若AE上有一动点P（不与A、E重合）自A点沿AE方向向E点匀速运动，运动的速度为每秒1个单位长度，设运动的时间为t秒（0＜t＜5），过P点作ED的平行线交AD于点M，过点M作AE的平行线交DE于点N．求四边形PMNE的面积S与时间t之间的函数关系式；t取何值时，S有最大值，最大值是多少？
（3）在（2）的条件下，当t为何值时，以A、M、E为顶点的三角形为等腰三角形，并求出相应时刻点M的坐标．

【题目】如图，在△ABC中，BC＝AC＝5，AB＝8，CD为AB边的高，点A在x轴上，点B在y轴上，点C在第一象限，若A从原点出发，沿x轴向右以每秒4个单位长的速度运动，则点B随之沿y轴下滑，并带动△ABC在平面内滑动，设运动时间为t秒，当B到达原点时停止运动.当△ABC的边与坐标轴平行时，t＝_____________.

【题目】如图，在□ABCD中，对角线AC、BD相交于点O，AB⊥AC，AB＝3cm，BC＝5cm.点P从A点出发沿AD方向匀速运动，速度为1cm/s.连结PO并延长交BC于点Q，设运动时间为t(0＜t＜5)．

(1)当t为何值时，四边形ABQP是平行四边形？

(2)设四边形OQCD的面积为y(cm2)，求y与t之间的函数关系式；

(3)是否存在某一时刻t，使点O在线段AP的垂直平分线上？若存在，求出t的值；若不存在，请说明理由．

　　备用图

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网