题目内容
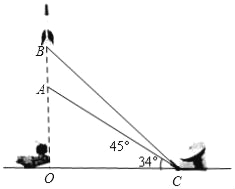
【题目】如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC,



(1)求C点的坐标;
(2)如图2,P为y轴负半轴上一个动点,当P点向y轴负半轴向下运动时,以P为顶点,PA为腰作等腰Rt△APD,过D作DE⊥x轴于E点,求OPDE的值;
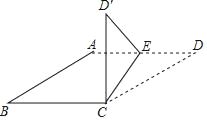
(3)如图3,已知点F坐标为(2,2),当G在y轴的负半轴上沿负方向运动时,作Rt△FGH,始终保持∠GFH=90,FG与y轴负半轴交于点G(0,m),FH与x轴正半轴交于点H(n,0),当G点在y轴的负半轴上沿负方向运动时,以下两个结论:①mn为定值;②m+n为定值,其中只有一个结论是正确的,请找出正确的结论,并求出其值.
【答案】(1)点C的坐标为(6,2); (2) OPDE= 2; (3)结论②是正确的,m+n=4.
【解析】
(1)过C点作CM⊥x轴于M点,因为AC=AB,则作CM⊥x轴,即求CM和AM的值,容易得△MAC≌△OBA,根据已知即可求得C点的值;
(2)求OPDE的值则将其放在同一直线上,过D作DQ⊥OP于Q点,即是求PQ的值,由图易求得△AOP≌△PDQ(AAS),即可求得PQ的长;
(3)利用(2)的结论,可知m+n为定长是正确的,过F分别作x轴和y轴的垂线,类似(2),即可求得m+n的值.
(1)过C作CM⊥x轴于M点,如图1,
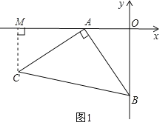
∵CM⊥OA,AC⊥AB,
∴∠MAC+∠OAB=![]() ,∠OAB+∠OBA=
,∠OAB+∠OBA=![]()
则∠MAC=∠OBA
在△MAC和△OBA中
则△MAC≌△OBA(AAS)
则CM=OA=2,MA=OB=4,则点C的坐标为(6,2);
(2)过D作DQ⊥OP于Q点,如图2,
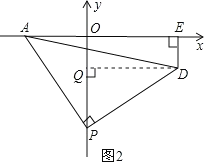
则OPDE=PQ,∠APO+∠QPD=![]() ,
,
∠APO+∠OAP=![]() ,则∠QPD=∠OAP,
,则∠QPD=∠OAP,
在△AOP和△PDQ中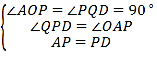
则△AOP≌△PDQ(AAS)
∴OPDE=PQ=OA=2;
(3)结论②是正确的,m+n=4,
如图3,过点F分别作FS⊥x轴于S点,FT⊥y轴于T点,

则FS=FT=2,∠FHS=∠HFT=∠FGT,
在△FSH和△FTG中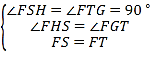
则△FSH≌△FTG(AAS)
则GT=HS,
又∵G(0,m),H(n,0),点F坐标为(2,2),
∴OT═OS=2,OG=|m|=m,OH=n,
∴GT=OGOT=m2,HS=OH+OS=n+2,
则2m=n+2,
则m+n=4.