Question

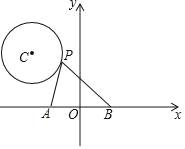
【题目】如图，已知直线y=-x+3与x轴、y轴分别交于A，B两点，抛物线y=-x2+bx+c经过A，B两点，点P在线段OA上，从点O出发，向点A以1个单位/秒的速度匀速运动；同时，点Q在线段AB上，从点A出发，向点B以个单位/秒的速度匀速运动，连接PQ，设运动时间为t秒．

（1）求抛物线的解析式；

（2）问：当t为何值时，△APQ为直角三角形；

（3）过点P作PE∥y轴，交AB于点E，过点Q作QF∥y轴，交抛物线于点F，连接EF，当EF∥PQ时，求点F的坐标；

（4）设抛物线顶点为M，连接BP，BM，MQ，问：是否存在t的值，使以B，Q，M为顶点的三角形与以O，B，P为顶点的三角形相似？若存在，请求出t的值；若不存在，请说明理由．

Answer 1

【答案】（1）y=-x2+2x+3；（2）t=1或t=；（3）点F的坐标为（2，3）．（4）．

【解析】

试题（1）先由直线AB的解析式为y=-x+3，求出它与x轴的交点A、与y轴的交点B的坐标，再将A、B两点的坐标代入y=-x2+bx+c，运用待定系数法即可求出抛物线的解析式；

（2）由直线与两坐标轴的交点可知：∠QAP=45°，设运动时间为t秒，则QA=t，PA=3-t，然后再图①、图②中利用特殊锐角三角函数值列出关于t的方程求解即可；

（3）设点P的坐标为（t，0），则点E的坐标为（t，-t+3），则EP=3-t，点Q的坐标为（3-t，t），点F的坐标为（3-t，-（3-t）2+2（3-t）+3），则FQ=3t-t2，EP∥FQ，EF∥PQ，所以四边形为平行线四边形，由平行四边形的性质可知EP=FQ，从而的到关于t的方程，然后解方程即可求得t的值，然后将t=1代入即可求得点F的坐标；

（4）设运动时间为t秒，则OP=t，BQ=（3-t），然后由抛物线的解析式求得点M的坐标，从而可求得MB的长度，然后根据相似相似三角形的性质建立关于t的方程，然后即可解得t的值．

试题解析：（1）∵y=-x+3与x轴交于点A，与y轴交于点B，

∴当y=0时，x=3，即A点坐标为（3，0），

当x=0时，y=3，即B点坐标为（0，3），

将A（3，0），B（0，3）代入y=-x2+bx+c，

得，解得

∴抛物线的解析式为y=-x2+2x+3；

（2）∵OA=OB=3，∠BOA=90°，

∴∠QAP=45°．

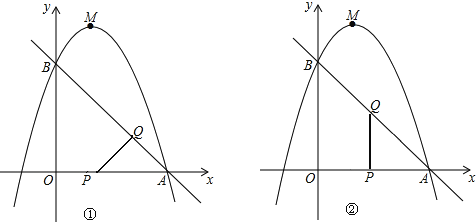
如图①所示：∠PQA=90°时，设运动时间为t秒，则QA=t，PA=3-t．

在Rt△PQA中，，即：，解得：t=1；

如图②所示：∠QPA=90°时，设运动时间为t秒，则QA=t，PA=3-t．

在Rt△PQA中，，即：，解得：t=．

综上所述，当t=1或t=时，△PQA是直角三角形；

（3）如图③所示：

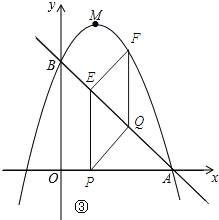
设点P的坐标为（t，0），则点E的坐标为（t，-t+3），则EP=3-t，点Q的坐标为（3-t，t），点F的坐标为（3-t，-（3-t）2+2（3-t）+3），则FQ=3t-t2．

∵EP∥FQ，EF∥PQ，

∴EP=FQ．即：3-t=3t-t2．

解得：t1=1，t2=3（舍去）．

将t=1代入F（3-t，-（3-t）2+2（3-t）+3），得点F的坐标为（2，3）．

（4）如图④所示：

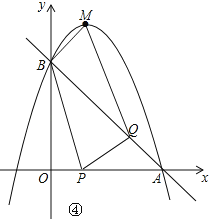
设运动时间为t秒，则OP=t，BQ=（3-t）．

∵y=-x2+2x+3=-（x-1）2+4，

∴点M的坐标为（1，4）．

∴MB=．

当△BOP∽△QBM时，即：，整理得：t2-3t+3=0，

△=32-4×1×3＜0，无解：

当△BOP∽△MBQ时，即：，解得t=．

∴当t=时，以B，Q，M为顶点的三角形与以O，B，P为顶点的三角形相似．