题目内容
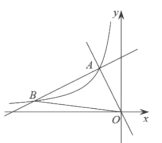
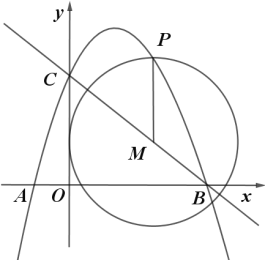
【题目】如图,抛物线y=ax2+![]() x+c经过点A(﹣1,0)和点C (0,3)与x轴的另一交点为点B,点M是直线BC上一动点,过点M作MP∥y轴,交抛物线于点P.
x+c经过点A(﹣1,0)和点C (0,3)与x轴的另一交点为点B,点M是直线BC上一动点,过点M作MP∥y轴,交抛物线于点P.
(1)求该抛物线的解析式;
(2)在抛物线上是否存在一点Q,使得△QCO是等边三角形?若存在,求出点Q的坐标;若不存在,请说明理由;
(3)以M为圆心,MP为半径作⊙M,当⊙M与坐标轴相切时,求出⊙M的半径.
【答案】(1)y=﹣![]() x2+
x2+![]() x+3;(2)不存在,理由见解析;(3)⊙M的半径为
x+3;(2)不存在,理由见解析;(3)⊙M的半径为![]() 或
或![]()
【解析】
(1)已知抛物线y=ax2+![]() x+c经过点A(﹣1,0)和点C(0,3),利用待定系数法即可求得抛物线解析式;
x+c经过点A(﹣1,0)和点C(0,3),利用待定系数法即可求得抛物线解析式;
(2)在抛物线上找到一点Q,使得△QCO是等边三角形,过点Q作OM⊥OB于点M,过点Q作QN⊥OC于点N,根据△QCO是等边三角形,求得Q点坐标,再验证Q点是否在抛物线上;
(3)分两种情况①当⊙M与y轴相切,如图所示,令M点横坐标为t,PM=t,将PM用t表示出来,列出关于t的一元二次方程,求得t,进而求得半径;②⊙M与x轴相切,过点M作MN⊥OB于N,如图所示,令M点横坐标为m,因为PN=2MN,列出关于m的一元二次方程,即可求出m,进而求得⊙M的半径.
(1)∵抛物线y=ax2+![]() x+c经过点A(﹣1,0)和点C(0,3)
x+c经过点A(﹣1,0)和点C(0,3)
∴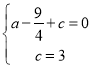
解得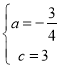
∴该抛物线的解析式为:y=﹣![]() x2+
x2+![]() x+3
x+3
故答案为:y=﹣![]() x2+
x2+![]() x+3
x+3
(2)在抛物线上找到一点Q,使得△QCO是等边三角形,过点Q作OM⊥OB于点M,过点Q作QN⊥OC于点N
∵△QCO是等边三角形,OC=3
∴CN=![]()
∴NQ=![]()
即Q(![]() ,
,![]() )
)
当x=![]() 时,y=﹣
时,y=﹣![]() ×(
×(![]() )2+
)2+![]() ×
×![]() +3=
+3=![]() ≠
≠![]()
∴Q(![]() ,
,![]() )不在抛物线上
)不在抛物线上
y=﹣![]() x2+
x2+![]() x+3
x+3

故答案为:不存在,理由见解析
(3)①⊙M与y轴相切,如图所示
∵y=﹣![]() x2+
x2+![]() x+3
x+3
当y=0时,﹣![]() x2+
x2+![]() x+3=0
x+3=0
解得x1=-1,x2=4
∴B(4,0)
令直线BC的解析式为y=kx+b
![]()
解得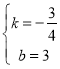
∴直线BC的解析式为![]()
令M点横坐标为t
∵MP∥y轴,⊙M与y轴相切
∴t=﹣![]() t2+
t2+![]() t+3-
t+3-![]()
解得t=![]()
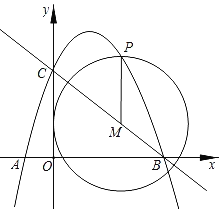
⊙M的半径为![]()
②⊙M与x轴相切,过点M作MN⊥OB于N,如图所示
令M点横坐标为m
∵PN=2MN
∴![]()
解得m=1或m=4(舍去)
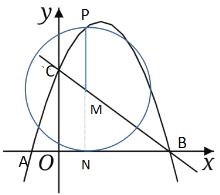
∴⊙M的半径为:
![]()
故答案为:⊙M的半径为![]() 或
或![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案