题目内容
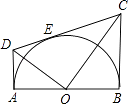
【题目】如图,在![]() ABCD中,AB⊥AC,AB=1,BC=
ABCD中,AB⊥AC,AB=1,BC=![]() ,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于E,F.
,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于E,F.
(1)求BD的长;
(2)当旋转角∠AOF=________° 时,△AOF与△BOE的面积相等?请写出理由.
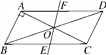
【答案】(1)![]() ;(2)90.
;(2)90.
【解析】(1)在Rt△ABC中,根据勾股定理求AC,由平行四边形性质求OA,在Rt△BAO中,由勾股定理得BO=![]() ;
;
(2)当F在AD中点时,OF和OE是△AOD和△BOC的中线,能平分面积,此时OF是三角形ABD的中位线,则OF平行于AB,所以∠AOF=∠BAC=90°.
解:(1)在Rt△ABC中,AB=1,BC=![]() ,
,
∴AC=![]() =2.
=2.
∵四边形ABCD为平行四边形,
∴BD=2BO,AO=![]() AC=1.在Rt△BAO中,由勾股定理得BO=
AC=1.在Rt△BAO中,由勾股定理得BO=![]() =
=![]() ,
,
∴BD=2![]() .
.
(2)90 理由如下:易证△BOE≌△DOF,
∴若△AOF与△BOE面积相等,则△AOF与△DOF面积相等.
又∵△AOF与△DOF底边AF和DF上的高相同,
∴AF=DF,即F为AD的中点.
又∵O为BD的中点,∴OF为△DAB的中位线,
∴OF∥AB,
∴∠AOF=∠BAC=90°.
故答案为90.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案【题目】甲、乙两名队员参加射击训练,成绩被分别绘制成如下两个统计图:
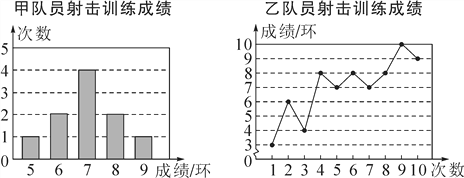
根据以上信息,整理分析数据如下:
平均成绩(环) | 中位数(环) | 众数(环) | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | 4.2 |
(1)则表格中a,b的值分别是a=________,b=________;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
【题目】列方程解应用题:五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 20 | 30 |
售价(元/件) | 29 | 40 |
(1)新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?