题目内容
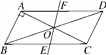
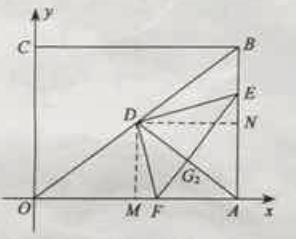
【题目】在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC,连结OB,D为OB的中点。点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF。已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒。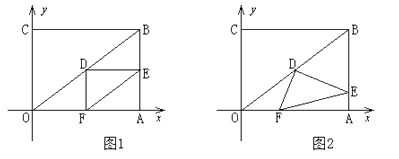
(1)如图1,当t=3时,求DF的长;
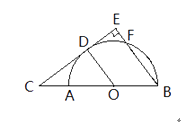
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值;
(3)连结AD,当AD将△DEF分成的两部分面积之比为1:2时,求相应t的值。
【答案】
(1)
解:当t=3时,如图1,点E为AB中点.
∵点D为OB中点,
∴DE//OA,DE=![]() OA=4,
OA=4,
∵OA⊥AB,
∴DE⊥AB,
∴∠OAB=∠DEA=90°,
又∵DF⊥DE,
∴∠EDF=90°
∴四边形DFAE是矩形,
∴DF=AE=3.
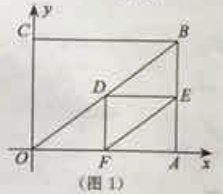
(2)
解: ∵∠DEF大小不变,如图2,
过D作DM⊥OA,DN⊥AB,垂足分别是M、N,
∵四边形OABC是矩形,
∴OA⊥AB,
∴四边形DMAN是矩形,
∴∠MDN=90°,DM//AB,DN//OA,
∴![]() ,
,![]() ,
,
∵点D为OB中点,
∴M、N分别是OA、AB中点,
∴DM=![]() AB=3,DN=
AB=3,DN=![]() OA=4,
OA=4,
∵∠EDF=90°,
∴∠FDM=∠EDN.
又∵∠DMF=∠DNE=90°,
∴△DMF∽△DNE
∴![]() ,
,
∵∠EDF=90°,
∴tan∠DEF=![]()
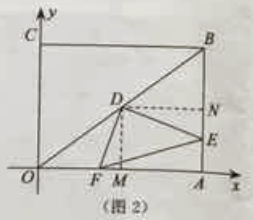
(3)
解:过D作DM⊥OA,DN⊥AB。垂足分别是M,N.
若AD将△DEF的面积分成1:2的两个部分,设AD交EF于点G,则易得点G为EF的三等分点.
①当点E到达中点之前时.
NE=3-t,由△DMF∽△DNE得
MF=![]() (3-t).
(3-t).
∴AF=4+MF=-![]() t+
t+![]() .
.
∵点![]() 为EF的三等分点。
为EF的三等分点。
∴![]() (
(![]() .
.![]() t).
t).
由点A(8,0),D(4,3)得直线AD解析式为y=-![]() χ+6.
χ+6.
![]() (
(![]() .
.![]() t)代入,得t=
t)代入,得t=![]() .
.
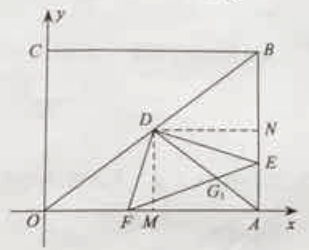
②当点E越过中点之后.
NE=t-3,由△DMF~△DNE得MF=![]() (t-3).
(t-3).
∴AF=4-MF=-![]() +
+![]() .
.
∵点![]() 为EF的三等分点.
为EF的三等分点.
∴![]() (
(![]() .
.![]() ).
).
代入直线AD解析式y=-![]() χ+6.
χ+6.
得t=![]() .
.
【解析】(1)当t=3时,如图1,点E、D分别为AB、OB中点,得出DE//OA,DE=![]() OA=4,根据OA⊥AB得出DE⊥AB,从而得出四边形DFAE是矩形,根据矩形性质求出DF=AE=3.
OA=4,根据OA⊥AB得出DE⊥AB,从而得出四边形DFAE是矩形,根据矩形性质求出DF=AE=3.
(2)如图2,过D作DM⊥OA,DN⊥AB,垂足分别是M、N,四边形OABC、DMAN都是矩形,由平行得出![]() ,
,![]() ,由D、M、N是中点又可以得出条件判断△DMF∽△DNE,从而得出tan∠DEF=
,由D、M、N是中点又可以得出条件判断△DMF∽△DNE,从而得出tan∠DEF=![]() 。
。
(3)过D作DM⊥OA,DN⊥AB。垂足分别是M,N;若AD将△DEF的面积分成1:2的两个部分,设AD交EF于点G,则易得点G为EF的三等分点.
分点E到达中点之前或越过中点之后来讨论,得出 NE,由△DMF∽△DNE得 MF和AF的长度, 再算出直线AD的解析式,由点G为EF的三等分点得出G点坐标将其代入AD直线方程求出t值。
【考点精析】本题主要考查了相似三角形的判定与性质和锐角三角函数的定义的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数才能正确解答此题.

【题目】丽水苛公司将“丽水山耕”农副产品运往杭州市场进行销售.记汽车行驶时间为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时) | 75 | 80 | 85 | 90 | 95 |
t(小时) | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从丽水出发,能否在上午10:00之前到达杭州市?请说明理由:
(3)若汽车到达杭州市场的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围.