题目内容
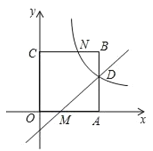
【题目】已知抛物线y=x2+bx+c经过点A(0,6),点B(1,3),直线l1:y=kx(k≠0),直线l2:y=-x-2,直线l1经过抛物线y=x2+bx+c的顶点P,且l1与l2相交于点C,直线l2与x轴、y轴分别交于点D、E.若把抛物线上下平移,使抛物线的顶点在直线l2上(此时抛物线的顶点记为M),再把抛物线左右平移,使抛物线的顶点在直线l1上(此时抛物线的顶点记为N).
(1)求抛物y=x2+bx+c线的解析式.
(2)判断以点N为圆心,半径长为4的圆与直线l2的位置关系,并说明理由.
(3)设点F、H在直线l1上(点H在点F的下方),当△MHF与△OAB相似时,求点F、H的坐标(直接写出结果).
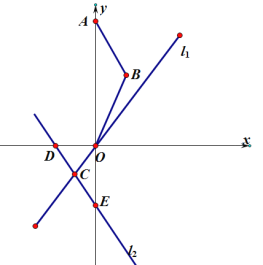
【答案】(1)![]() ;(2)以点
;(2)以点![]() 为圆心,半径长为4的圆与直线
为圆心,半径长为4的圆与直线![]() 相离;理由见解析;(3)点
相离;理由见解析;(3)点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() 或
或![]() 、
、![]() 或
或![]() 、
、![]() .
.
【解析】
(1)分别把A,B点坐标带入函数解析式可求得b,c即可得到二次函数解析式
(2)先求出顶点![]() 的坐标,得到直线
的坐标,得到直线![]() 解析式,再分别求得MN的坐标,再求出NC比较其与4的大小可得圆与直线
解析式,再分别求得MN的坐标,再求出NC比较其与4的大小可得圆与直线![]() 的位置关系.
的位置关系.
(3)由题得出tan![]() BAO=
BAO=![]() ,分情况讨论求得F,H坐标.
,分情况讨论求得F,H坐标.
(1)把点![]() 、
、![]() 代入
代入![]() 得
得![]() ,
,
解得,![]() ,
,
∴抛物线的解析式为![]() .
.
(2)由![]() 得
得![]() ,∴顶点
,∴顶点![]() 的坐标为
的坐标为![]() ,
,
把![]() 代入
代入![]() 得
得![]() 解得
解得![]() ,∴直线
,∴直线![]() 解析式为
解析式为![]() ,
,
设点![]() ,代入
,代入![]() 得
得![]() ,∴得
,∴得![]() ,
,
设点![]() ,代入
,代入![]() 得
得![]() ,∴得
,∴得![]() ,
,
由于直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]()
∴易得![]() 、
、![]() ,
,
∴![]() ,
,![]()
∴![]() ,∵点
,∵点![]() 在直线
在直线![]() 上,
上,
∴![]() ,
,
∴![]() ,
,![]() 即
即![]() ,
,
∵![]() ,
,
∴以点![]() 为圆心,半径长为4的圆与直线
为圆心,半径长为4的圆与直线![]() 相离.
相离.
(3)点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() 或
或![]() 、
、![]() 或
或![]() 、
、![]() .
.
C(-1,-1),A(0,6),B(1,3)
可得tan![]() BAO=
BAO=![]() ,
,
情况1:tan![]() CF1M=
CF1M= ![]() =
= ![]() ,
, ![]() CF1=9
CF1=9![]() ,
,
M F1=6![]() ,
,![]() H1F1=5
H1F1=5![]() ,
,![]() F1(8,8),H1(3,3);
F1(8,8),H1(3,3);
情况2:F2(-5,-5), H2(-10,-10)(与情况1关于L2对称);
情况3:F3(8,8), H3(-10,-10)(此时F3与F1重合,H3与H2重合).