��Ŀ����
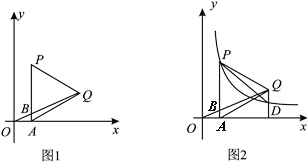
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������OABC�Ķ���O������ԭ���غϣ���C������Ϊ��0��3������A��x����������ϣ�ֱ��y��x��1����AB��OA�ڵ�D��M������������![]() ��ͼ����D����BC�Ľ���ΪN��
��ͼ����D����BC�Ľ���ΪN��
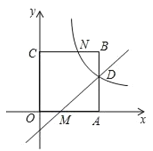
��1����BN�ij���
��2����P��ֱ��DM�ϵĶ��㣨��P�����D����M�غϣ�������PB��PC��MN������BCP����������ı���ABNM�����ʱ�����P�����꣮
��3���ڣ�2���������£�����CP����CPΪ��������CPEF��ʹ���εĶԽ��ߵĽ���G����ֱ��DM�ϣ���д����G�����꣮
���𰸡���1��1 ��2����7��6�� ��3����![]() ��
��![]() ��
��
��������
��1���������ε����ʿɵó���A��B�����꣬����һ�κ���ͼ���ϵ�����������ɵó���D�����꣬�ɵ�D�����꣬���ô���ϵ�����������������������ʽ�������÷���������ͼ���ϵ�����������ɵó���N�����꣬��ϵ�B����������BN�ij���
��2������һ�κ���ͼ���ϵ�����������ɵó���M�����꣬�������ε������ʽ���������ABNM����������P������Ϊ��x��x-1����x��1��x��3�������������ε������ʽ��ϡ�BCP�������������ABNM����������ɵó�����x�ĺ�����ֵ���ŵ�һԪһ�η��̣���֮���ɵó����ۣ�
��3������C��CF��CP����DM�ڵ�F�����F������Ϊ��n��n-1������ϵ�C��P�����꣬���������ľ��빫ʽ�����![]() ��ֵ�����ù��ɶ����ɵó�����n��һԪһ�η��̣���֮���ɵó���F�����꣬�ٽ�ϵ�GΪ�߶�PF���е㣬���������G�����꣮
��ֵ�����ù��ɶ����ɵó�����n��һԪһ�η��̣���֮���ɵó���F�����꣬�ٽ�ϵ�GΪ�߶�PF���е㣬���������G�����꣮
�⣺��1��![]() ������OABC
������OABC
![]() ��A��������3��0������B��������3��3����
��A��������3��0������B��������3��3����
![]() ��x��3ʱ��y��x��1��2��
��x��3ʱ��y��x��1��2��
���D��������3��2����
��D��3��2������![]() ���ã�
���ã�![]() ����ã�m��6��
����ã�m��6��
�෴������������ʽΪ![]() ��
��
��y��3ʱ��![]() ����ã�x��2��
����ã�x��2��
���N��������2��3����
��BN��3��2��1��
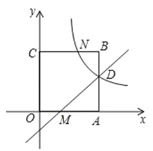
��2����y��0ʱ��x��1��0����ã�x��1��
���M��������1��0����
��AM��2��
![]() ����AMNB
����AMNB![]() ��
��
��ͼ1�����P������Ϊ��x��x��1����x��1��x��3����
![]() ,
,
��ã�![]() ����ȥ����
����ȥ����![]() ��
��
���P��������7��6����
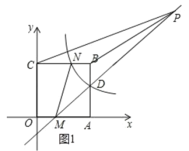
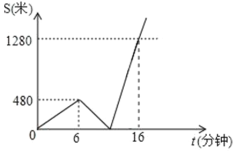
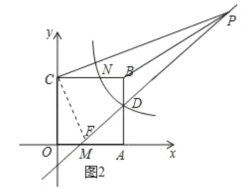
��3������C��CF��CP����DM�ڵ�F��
��ͼ2��ʾ�����F������Ϊ��n��n��1����
�ߵ�C������Ϊ��0��3������P������Ϊ��7��6����
��![]()
![]()
![]()
�ߡ�PCF��90����
��![]() ��
��
��![]()
��ã�![]() ��
��
���F��������![]() ����
����
�֡ߵ�GΪ���ζԽ��ߵĽ��㣬
![]() GΪ�߶�PF���е㣬
GΪ�߶�PF���е㣬
���G��������![]() ����
����

 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�����Ŀ��ij���мƻ������ס���������Ʒ��������Ʒ�Ľ��ۡ��ۼ����±���
��Ʒ | �� | �� |
���ۣ�Ԫ/���� | x60 | x |
�ۼۣ�Ԫ/���� | 200 | 100 |
����1800Ԫ����������Ʒ�ļ�������900Ԫ����������Ʒ�ļ�����ͬ��
��1����ס���������Ʒ�Ľ����Ƕ���Ԫ��
��2�����������ۼס���������Ʒ��100�����������ۼ�����ƷΪa����a40������������100���ס���������Ʒ��������ΪwԪ����w��a֮��ĺ�����ϵʽ�������w����Сֵ��