题目内容
【题目】已知:如图,四边形ABCD和四边形AECF都是矩形,AE与BC交于点M,CF与AD交于点N.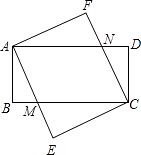
(1)求证:△ABM≌△CDN;
(2)矩形ABCD和矩形AECF满足何种关系时,四边形AMCN是菱形,证明你的结论.
【答案】
(1)
证明:∵四边形ABCD是矩形,
∴∠B=∠D=90°,AB=CD,AD∥BC,
∵四边形AECF是矩形,∴AE∥CF,
∴四边形AMCN是平行四边形,
∴AM=CN,
在Rt△ABM和Rt△CDN中,
∵ ![]() ,
,
∴Rt△ABM≌Rt△CDN(HL)
(2)
解:当AB=AF时,四边形AMCN是菱形,
理由:∵四边形ABCD、AECF是矩形,
∴∠B=∠BAD=∠EAF=∠F=90°,
∴∠BAD﹣∠NAM=∠EAF﹣∠NAM,即∠BAM=∠FAN,
在△ABM和△AFN中∠BAM=∠FAN,AB=AF,∠B=∠F
∵ 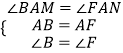 ,
,
∴△ABM≌△AFN(ASA),
∴AM=AN,
由(1)知四边形AMCN是平行四边形,
∴平行四边形AMCN是菱形.
【解析】(1)利用矩形的性质结合平行四边形的判定于性质得出AM=CN,进而得出Rt△ABM≌Rt△CDN;(2)利用全等三角形的判定得出△ABM≌△AFN(ASA),进而得出四边形AMCN是菱形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目